1. Lesson 5

1.5. Explore 4

Mathematics 30-2 Module 7

Module 7: Exponents and Logarithms

 

In Try This 2, you may have found that the logarithm of a power can be rewritten as the product of a number and a logarithm using the law logb (Mn)= n logb M. The following explains the relationship between this law and the power law of powers:

 

power law of logarithms logb (Mn)= n logb M In the product law of powers, (bm)n = bm × n, the exponents are multiplied. In the power law of logarithms, logb (Mn)= n logb M, when you have a power in a single logarithm, it is the same as multiplying the exponent to the logarithm of the base of the power.


tip

One way of thinking of the rule logb (Mn)= n logb M is that the value n can be moved from the exponent position to become the coefficient of the log and vice versa.

 

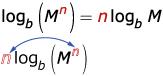
This diagram shows the power law of logarithms. Below it is written n times the base b logarithms of M to the power of n. Both n’s are red outlines with a double-headed arrow between them.



Here are some numeric examples of the power law of logarithms:

 

 

log6 24 = 4 log6 2
 
 
 



The power law of logarithms is useful when trying to solve exponential equations. Lesson 6 will explore this idea.

 

Self-Check 2



textbook

Complete questions 5.b., 7.b., 7.d., 9, and 15 on pages 446 and 447 of your textbook. Answer

 

 


textbook

Add the following to your copy of Formula Sheet:

  • logb M + logb N = logb(M × N)
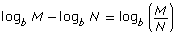
  • logb (Mn) = n logb M