1. Module 1

1.37. Page 2

Module 1: Lesson 7

Module 1—Thinking Energy

Explore

 

Read

 

reference energy state: a reference point at which the potential energy of the elements in their most stable form at SATP is defined as zero

 

standard enthalpy of formation: the enthalpy change calculated from the measurements of a formation reaction under standard conditions

In previous lessons you may have noticed the difference between the symbols ΔrHº and ΔrH. The degree symbol means that a reaction enthalpy or other property of a system was measured at a standard state. A standard state is a defined set of conditions. You may recall learning two sets of standard conditions when working with gases: STP and SATP.

 

Read the first two paragraphs on page 510 in the textbook to learn more about the standard used in enthalpy determinations. Take note of the definitions for reference energy state and standard enthalpy of formation.

 

Self-Check
 

SC 1. Using an energy diagram, explain how defining elements as having a standard enthalpy of formation allows for the determination of standard enthalpies of formation for compounds.

 

Check your work.
Self-Check Answers

 

Contact your teacher if your answers vary significantly from the answers provided here.
 
SC 1.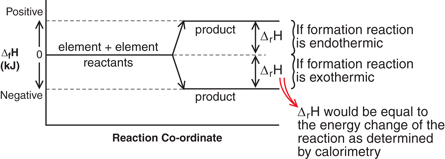

 

 

Read

 

thermal stability: the tendency of a compound to resist decomposition when heated

 

The lower a compound's standard enthalpy of formation, the more stable the compound.

Read the remainder of page 510 in the textbook to learn about the concept of thermal stability. Keep an image of an energy diagram fresh in your mind as you read.

 

Does the analogy stated in the textbook make sense to you? Which substance has greater thermal stability: octane (ΔfHmº = −250.1 kJ/mol) or trinitrotoluene (TNT, ΔfHmº = +123.6 kJ/mol)? Is your conclusion consistent with the reputations of these two compounds?

 

Read

 

Work through “Sample problem 11.5” on page 511 of the textbook to see how molar enthalpies of formation can be used to calculate enthalpies of reaction. You may also wish to read pages 512–513.

 

Self-Check

 

SC 2. Complete “Section 11.5” questions 2 and 3 on page 514 of the textbook.

 

Check your work.
Self-Check Answers

 

Contact your teacher if your answers vary significantly from the answers provided here.

 

SC 2.

 

Section 11.5 2.

  1.  

    Reactants

    Products

    Species

    CH4(g)

    H2O(g)

    CO(g)

    H2(g)

    Coefficient (mol)

    1

    1

    1

    3

    ΔfHmº (kJ/mol)

    −74.6

    −241.8

    −110.5

    0

    Σ n ΔfHmº

    = [(1 mol × −74.6 kJ/mol)

          + (1 mol × −241.8 kJ/mol)]
    = −316.4 kJ

    = [(1 mol × −110.5 kJ/mol)

          + (3 mol × 0 kJ/mol)]
    = −110.5 kJ

    ΔrHº

    = −110.5 kJ − (−316.4 kJ)
    = +205.9 kJ


  2.  

    Reactants

    Products

    Species

    CO(g)

    H2O(g)

    CO2(g)

    H2(g)

    Coefficient (mol)

    1

    1

    1

    1

    ΔfHmº (kJ/mol)

    −110.5

    −241.8

    −393.5 kJ

    0

    Σ n ΔfHmº

    = [(1 mol × −110.5 kJ/mol)

          + (1 mol × −241.8 kJ/mol)]
    = −352.3 kJ

    = [(1 mol × -393.5 kJ/mol)

          + (1 mol × 0 kJ/mol)]
    = −393.5 kJ

    ΔrHº

    = −393.5 kJ − (−352.3 kJ)
    = −41.2 kJ


  3.  

    Reactants

    Products

    Species

    N2(g)

    H2(g)

    NH3(g)

     

    Coefficient (mol)

    1

    3

    2

     

    ΔfHmº (kJ/mol)

    0

    0

    −45.9

     

    Σ n ΔfHmº

    = [(1 mol × 0 kJ/mol)

          + (3 mol × 0 kJ/mol)]
    = 0 kJ

    = (2 mol × −45.9 kJ/mol)
    = −91.8 kJ

    ΔrHº

    = −91.8 kJ − (0 kJ)
    = −91.8 kJ
Section 11.5 3.

  1.  

    Reactants

    Products

    Species

    NH3(g)

    O2(g)

    NO(g)

    H2O(g)

    Coefficient (mol)

    4

    5

    4

    6

    ΔfHmº (kJ/mol)

    −45.9

    0

    +91.3

    −241.8

    Σ n ΔfHmº

    = [(4 mol × −45.9 kJ/mol)

          + (5 mol × 0 kJ/mol)]
    = −183.6 kJ

    = [(4 mol × +91.3 kJ/mol)

          + (6 mol × −241.8 kJ/mol)]
    = −1085.6 kJ

    ΔrHº

    = −1085.6 kJ − (−183.6 kJ)
    = −902.0 kJ




  2.  

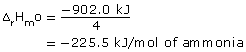
    Reactants

    Products

    Species

    NO(g)

    O2(g)

     NO2(g)

     

    Coefficient (mol)

    2

    1

    2

     

    ΔfHmº (kJ/mol)

    +91.3

    0

    +33.2

     

    Σ n ΔfHmº

    = [(2 mol × +91.3 kJ/mol)

          + (1 mol × 0 kJ/mol)]
    = +181.6 kJ

    = (2 mol × +33.2 kJ/mol)
    = +66.4 kJ

    ΔrHº

    = +66.4 kJ − (+181.6 kJ)
    = −116.2 kJ




  3.  

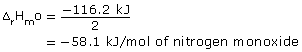
    Reactants

    Products

    Species

    NO2(g)

    H2O(g)

    HNO3(l)

    NO(g)

    Coefficient (mol)

    3

    1

    2

    1

    ΔfHmº (kJ/mol)

    +33.2

    −285.8

    −174.1

    +91.3

    Σ n ΔfHmº

    = [(3 mol × +33.2kJ/mol)

          + (1 mol × −285.8 kJ/mol)]
    = −186.2 kJ

    = [(2 mol × −174.1 kJ/mol)

          + (1 mol × +91.3 kJ/mol)]
    = −256.9 kJ

    ΔrHº

    = −256.9 kJ − (−186.2 kJ)
    = −70.7 kJ


 

Self-Check

 

In the previous Self-Check activity you used the standard molar enthalpies of formation for compounds to predict the reaction enthalpy. Can this process be reversed?

 

If given a reaction enthalpy, most likely determined by experiment, a standard molar enthalpy of formation for a species in the reaction can be determined as long as the standard molar enthalpies of formation for the other species are known.

 

SC 3. Calculate the standard molar enthalpy of formation for hexane, C6H14(l). Assume that hexane’s standard molar enthalpy of combustion is −4162.9 kJ/mol.

 

Check your work.
Self-Check Answers

 

Contact your teacher if your answers vary significantly from the answers provided here.

 

SC 3.

 

Balanced Reaction Equation

 

C6H14(l) + 19/2 O2(g) → 6 CO2(g) + 7 H2O(g) ΔrHmº = –4162.9 kJ/mol C6H14(l)

 

ΔrHº = –4162.9 kJ/mol x 1 mol C6H14(l)

       = –4162.9 kJ

 

 

Reactants

Products

ΔrHº

Species

C6H14(l)

O2(g

CO2(g)

H2O(g)

 

Coefficient (mol)

1

19/2

6

7

 

ΔfHmº (kJ/mol)

?

0

–393.5

–241.8

 

Σ n ΔfHmº

= [(1 mol × ΔfHmº(hexane))       + (19/2 mol × 0 kJ/mol)]
= 1 mol × ΔfHmº(hexane)

= [(6 mol × −393.5 kJ/mol)

      + (7 mol × −241.8 kJ/mol)]
= −4053.6 kJ

−4162.9 kJ

 

−4053.6 kJ − (1 mol × ΔfHmº(hexane)) = −4162.9 kJ

 

ΔfHmº(hexane) = +109.3 kJ/mol

 

The standard molar enthalpy of formation for hexane is +109.3 kJ/mol.

 

Reflect on the Big Picture

 

Standard molar enthalpies of formation allow for quick predictions of reaction enthalpies. Using the hiking analogy introduced in Lesson 7, these values provide an estimate of the chemical potential energy of each compound in the reaction equation. The difference between the potential energies of the products and the reactants is the reaction enthalpy. Using standard molar enthalpies of formation is a lot like knowing the checkpoints you must reach along your hike.

 

RBP 1. How would you use information on standard molar enthalpies of formation in your ecotour planning? Identify a situation in which this method of determining reaction enthalpy could be used. Identify where other methods and techniques learned in Module 1 could be applied to the operation of your ecotour.

 

Save a copy of your response in your ecotour planning sub-folder. This is the last of six assignments that you can submit as part of your Module 1 Assessment. For more information refer to the Module 1 Assessment.

 

Module 1: Lesson 8 Assignment

 

Retrieve your copy of the Module 1: Lesson 8 Assignment that you saved to your computer earlier in this lesson. Complete the Assignment. Save a copy of your completed Assignment in your course folder and submit a copy to your teacher.