Module 2
1. Module 2
1.4. Page 2
Module 2—The Conservation of Momentum in Isolated Systems
 Explore
Explore
 Read
Read
Read “Collisions in One Dimension” on pages 468 to 470 of your physics textbook for an introduction to collisions of systems of objects.
Understanding Isolated and Non-isolated Systems

Lawrence M. Sawyer / Sports and Recreation 2/Getty Images
A system is a collection of two or more objects. For example, a collection of curling stones on a sheet of ice represents a system. If the number of stones on the ice does not change, the system is closed. If there were no external forces acting on the stones, such as the players pushing them or the small amount of friction on the ice, the system would also be isolated.
There are other kinds of systems as well, some of which you may be familiar with.
In the open system, mass and energy may enter or leave the system, and external forces may influence the system. In the closed system, no mass enters or leaves the system but energy can. Also, external forces may influence the closed system. No net external force acts on the isolated system, and no mass or energy enters or leaves the system.
|
|---|
A truly isolated system is impossible to create. Isolating a system in terms of mass is fairly straightforward. However, isolating the system with respect to energy and external forces, especially gravity, is far more difficult. For questions in Physics 30 it is assumed that the system is isolated from net external forces in order to simplify questions.
|
In this lesson when we examine the momentum of a system, it is important that the system under investigation is an isolated system. Assumptions are often made that the force of friction acting in a system is negligible, thereby providing a useful model for approximating real world situations, such as vehicle collisions.
It is easy to tell if a system is closed: no mass enters or exits. However, it is a bit more difficult to determine if a system is isolated—you must be aware of any external forces that may be acting on the system. Here are some examples:
Example 1
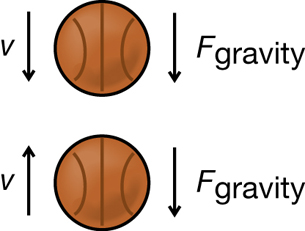
Two basketballs (the system) are moving vertically in the air. One of the balls is falling down, while the other has just been thrown upward. The two balls collide as they move.
The system is not isolated. The external force acting on both balls is the force of gravity.
Example 2
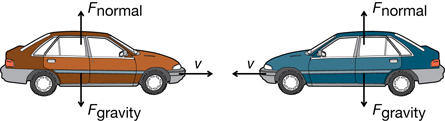
Two cars (the system) are driving toward one another on smooth pavement and collide head on.
If we assume that the force of friction is negligible, this system can be treated as isolated. Interestingly, in the vertical plane, the normal force of the road balances the force of gravity, so there is no net external force in the vertical plane.
Example 3
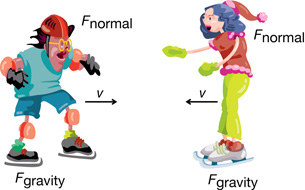
Two skaters (the system) are coasting along frictionless ice and are headed straight for each other. They end up crashing into each other.
If we assume that the force of friction is negligible, this system can be treated as isolated. Again, there is no net external force acting in the vertical plane.
Module 1: Lesson 1 explained that any moving object has velocity and momentum. But what happens if two or more objects collide? What happens to the velocity and the momentum of each object? Let’s explore this question using a simulation of a rear-end collision.