1. Module 2

1.6. Page 4

Lesson 1

Module 2—The Conservation of Momentum in Isolated Systems

The Law of Conservation of Momentum


For any isolated system, the total momentum does not change. In a collision, momentum is conserved—the total momentum before the collision is equal to the total momentum after the collision. Expressed as an equation, the law of conservation of momentum is

 


sum of initial momentum = sum of final momentum

 

The conservation principle can also be expressed algebraically as follows:

 

 

An image of Newton’s cradle is shown.

© Djordje Komljenovic/shutterstock

The law of conservation of momentum governs all physical interactions. It is considered to be one of the fundamental laws of physics. The law has been used to investigate and analyze all types of interactions. In addition to vehicle accidents, it has been used in the study of subatomic particles, such as electrons and protons, all the way up to the astronomical study of planets, stars, and galaxies.

 

This law controls the universe by keeping the total quantity of motion in the universe fixed. That is, if one body slows down and comes to rest, another body must speed up and start moving. Newton’s cradle of swinging masses is a good example of this, as you can see in the picture on the right.

 

Watch and Listen

 

View The Conservation of Momentum video, which describes how Rene Descartes’ knowledge of straight lines led him to develop the law of conservation of momentum.

 

Analyzing Collisions

 

In the lab section you discovered that the total momentum of a system is conserved, as long as there are no external forces acting on a system. The conservation of momentum will be used to analyze various collisions. When solving problems, it is useful to follow the GRASP model for problem solving.

 

The GRASP model is on page 867 in your textbook.

 

Self-Check

 

Verify your answers, where possible, by using the Collision 1D simulator.

 

SC 1. A 5.0-kg object is travelling to the right at 10.0 m/s. It collides with a 7.0-kg object that initially is at rest. After the collision, the 5.0-kg object continues to move to the right, but at 1.17 m/s. In what direction and with what speed is the other object moving?

 

Check your work.
Self-Check Answers

 

SC 1.

 

Given

 

mass 1 m1 = 5.0 kg

mass 2 m2 = 7.0 kg
mass 1 initial velocity
mass 2 initial velocity
mass 1 final velocity

 

Required

 

The final velocity of the 7.0-kg object .

 

Analysis and Solution

 

Choose the two objects as an isolated system. Since the 7.0-kg object is stationary, its initial momentum is 0.

 

 
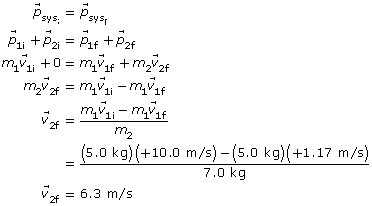
Paraphrase

 

The final velocity of the 7.0-kg object is 6.3 m/s.