Module 3
1. Module 3
1.33. Page 4
Module 3—Electrical Phenomena
Part B: Storing Potential Energy in a Non-Uniform Electric Field
Purpose
In this part of the lab activity you will continue to use electric field potential, non-uniform simulation to collect data enabling you to answer the following question:
- In which direction must a test charge be moved within an electric field if potential energy is to be stored in the system?
Procedure
Step 1: If you still have the computer simulation open from Part A of this lab activity, continue with the next step. If you need to re-open the simulation, you will need to enter the settings described in Part A.
Step 2: To return the particle to its initial position, (100,0), press “rewind” (
). Press “data” (
) to view a data chart describing the particle, as well as a set of bar graphs of potential energy (in blue), kinetic energy (in red), and voltage (in yellow).
If these settings have been applied the screen should look like these settings:
Step 3: Press “play” (
), and observe the changing energy values until the test charge reaches the point (x,y) = (300,0). Then press “pause” (
). You may simply press “rewind” () to return the test charge to its starting position if you need to try again. Collect the following data, which you will use in the Analysis, for these two locations:
Data for the Test Charge at (100,0) |
Data for the Test Charge at (300,0) |
Kinetic Energy = Ek = |
Kinetic Energy = Ek= |
Potential Energy = Ep = |
Potential Energy = Ep= |
Total Energy = Etotal = |
Total Energy = Etotall = |
Step 4: Even though you will be properly introduced to voltage later in this lesson, this is a good opportunity to gather voltage data from the simulation. You will use this voltage data in the Analysis. Collect the following additional data for these two locations:
Data for the Test Charge at (100,0) |
Data for the Test Charge at (300,0) |
Potential Energy = Ep = |
Potential Energy = Ep = |
Test Charge = qtest = |
Test Charge = qtest= |
Voltage = V = |
Voltage = V = |
Step 5: Return the particle to its initial position, (100,0), by pressing “rewind” (). Enter the highest value of initial velocity that the simulation will accept, 30.0 m/s. Press “play” (), and let the simulation run in the background while you answer the next three questions.
Analysis
Self-Check
SC 4.
- As the test charge moves from (100,0) to (300,0), calculate the change in the potential energy, kinetic energy, and the total energy.
- Identify the physics principle that explains your results in SC 4.a.
SC 5. If the test charge were to be moved toward the source from (300,0) to (100,0) work would have to be done. The applied force would have to overcome the electrostatic force at each point between (300,0) and (100,0).
- Explain the difficulties in using the equation
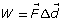to solve for the work in this case.
- Use the idea that the potential energy is equal to the work done to change the position of an object to solve for the work in this case.
SC 6. Press “pause” (), and record the following values:
- position of the test charge: (x,y) = (________ m, __________ m)
- potential energy of the system = ____________
The simulation does not display potential energy values less than 1 J. If the system could display values of potential energy that were in millijoules or even in microjoules, you would be waiting forever for the potential energy of the system to reach zero. That’s because potential energy is defined to be zero at infinity—it takes an infinitely long time for a particle to move infinitely far away. Speculate on why infinity was chosen as the reference point having zero potential energy for this system.
Self-Check Answers
SC 4.
a.
| Initial Energy Values at (100,0) | Final Energy Values at (300,0) | Change in Energy Values (ΔE = Ef – Ei ) |
|---|---|---|
Ek = 338 J |
Ek = 697 J |
ΔEk = 359 J |
Ep = 539 J |
Ep = 180 J |
ΔEp = –359 J |
Etotal = 877J |
Etotal = 877 J |
ΔEtotal = 0 |
b. The results in the previous answer can be explained using the law of conservation of energy. The gain in the kinetic energy of the test charge accounted for by the loss of an identical amount of potential energy.
SC 5.
- The difficulty with this equation is that the value for the applied force changes continually to match the continual changes in the electrostatic force. The electrostatic force would increase as the test charge moves closer to the source charge.
Given
The location (300,0) is the initial position.
The location (100,0) is the final position.
Required
The work done to move the charge from 300 m to 100 m.
Analysis and Solution
The change in the potential energy of the system is equal to the work done to change the position of the test charge.
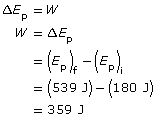
Paraphrase
The work done to move the test charge from 300 m to 100 m is 359 J.
SC 6. The data you collected for the position of the test charge and the potential energy will vary depending on how long you let the simulation run. Your data should reflect a large separation between the test charge and the source charge of the field. That is, you should have observed a large value of x in the test-charge position (x, y). The y value should not change much, if at all, from 0.
The potential energy you record should be close to, or possibly equal to, 0 J.
There is good reason for choosing infinity as the reference point having zero potential energy. This reference point works for virtually all charges in virtually all circumstances, even if the system being studied has more than one source charge. If some other reference point were chosen as a reference point, such as the surface of a source charge, then you’d have to choose which source charge would provide the reference point for the system.
Part B Conclusion
Module 3: Lesson 5 Assignment
Remember to submit the answer to LAB 3 to your teacher as part of your Module 3: Lesson 5 Assignment.
LAB 3. In which direction must a test charge be moved within an electric field if potential energy is to be stored in the system? Why?