1. Module 3

1.34. Page 5

Module 3 Lesson 5

Module 3—Electrical Phenomena

 

Storing and Releasing Potential Energy

 

Two photographs are shown side by side. The photo on the left shows a BASE jumper leaping toward Earth. The photo on the right shows bubbles being repelled by a Van de Graaff generator.

© Vasily Smirnov/shutterstock (jumper)


Both of these photos show objects accelerating in fields. The BASE jumper is accelerating to Earth due to the force of gravity acting through Earth’s gravitational field. The charged soap bubbles are accelerating away from the charged globe of the Van de Graaff generator due to the electrostatic force acting through the electric field of the Van de Graaff generator. In both cases, potential energy stored in the system is being transformed into kinetic energy.

 

Read

 

You can find out more about the similarities between the potential energy stored in these two situations by reading pages 560 to 562 of your textbook. Pay special attention to “Example 11.5” and to the connections to the previous lab activity.

 

Self-Check

 

SC 7.

  1. Define electric potential energy.

  2. Solve “Practice Problem” 2 on page 561 of your textbook.

  3. Explain why it is important to indicate the reference position when stating a value for potential energy.

SC 8. When it comes to calculations, the textbook uses a particular method for defining the reference point for electric potential energy. Describe this method, and relate it to your experiences with the simulation in the previous lab activity.

 

Check your work.
Self-Check Answers

 

SC 7.

  1. Electric potential energy is the energy stored in a system when work is done to move a charge from one location to another.

Given

 

 

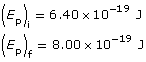
Required

 

The work necessary to move the charge.

 

Analysis and Solution

 

 

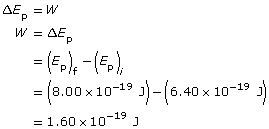
Paraphrase

 

The work to move the charge is 1.60×10−19 J.

  1. Potential energy is equal to the work done to change the position of an object. This only makes sense if you know the reference level where potential energy is defined to be zero. The reference level is the starting point for the displacement vector in the work calculation.

SC 8. The textbook uses the method where electric potential energy is defined to be zero at infinity. In other words, infinity is the reference level. When the simulation was allowed to run for nearly 20 minutes, the potential energy of the system dropped to a value of 1 J when the distance from the source was very large. It appears that the simulation uses the same method of defining the electric potential energy to be zero at infinity

 

 

Electric Potential or Voltage

 

The following diagram summarizes some of the key findings from the previous lab investigation.

 

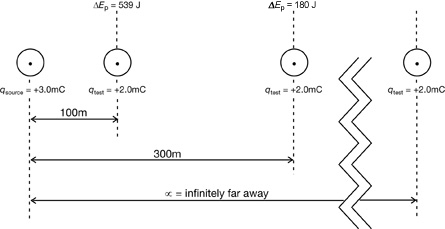
This illustration shows the key data collected for a test charge as it is moved closer to a source charge.

 

It takes 180 J of work to move a positive test charge from a point infinitely far away to a location 300 m from the source charge. Since this work was done against the electric field, the electric potential energy of the system is 180 J at this point. Note that electric potential energy is defined to be zero at infinity.

 

It takes even more work, 539 J, to move the same positive test charge from a point infinitely far away to a location 100 m from the source charge. The electric potential energy of the system is said to be 539 J at this point.

 

voltage: the value, in volts, of the change in electric potential energy stored per unit of charge.

 

It is also called electric potential or potential difference.

Although this system accurately describes the situation, it is impractical to make these sorts of measurements in practice. Measuring the work done moving tiny particles with minute amounts of charge is a problem. A more practical way to describe these situations is to use a new quantity called voltage (or electric potential).

 

Expressed as an equation,

 

 

Quantity

Symbol

SI Unit

change in electric potential energy

ΔEp

J

charge

q

C

voltage or
electric potential

V

V

 

Note that 1 volt is the electrical potential at a given point in an electric field such that 1 joule of energy is required to move 1 coulomb of charge from infinity to that point.

 

1 V = 1 J/C

 


 

Try This

 

TR 1. The volt is not a base SI unit. Break the volt down into C, kg, m, and s.

 

The following graphic illustrates how the voltage would be calculated for the results of the previous lab activity:

 

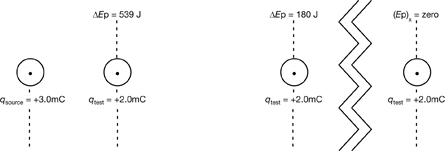
This illustration shows the key data collected for a test charge as it is moved closer to a source charge.

 

The number of volts describes the amount of energy required to move a coulomb from infinity to each location in the field—a value of “90 000 volts” means “90 000 joules per coulomb.”

 

Self-Check

 

SC 9. Suppose the test charge shown in the previous diagram was +4.0 mC instead of +2.0 mC.

  1. Explain how this new value for the test charge would affect the amount of work required to move the test from infinity to each location.

  2. Given your answer from SC 9.a., explain how this new value for test charge would affect the value of the voltage at each location.

  3. Does the value of the voltage depend upon the value of the test charge?
Check your work.
Self-Check Answer

 

SC 9.

  1. If the charge on the test body were doubled, then it would take twice as much work to move the test body from infinity to each location. Even though the displacement values would remain unchanged, doubling the charge would double the electrostatic force, which would double the amount of work required.

  2. Voltage is the change in electrical potential energy per unit of charge. Doubling the charge also doubles the electrical potential energy stored in the system since the work done on the charge doubles. The overall effect is that the voltage would be unchanged.

  3. No, the value of the voltage is independent of the charge. This is demonstrated in the answer to SC 9.b.