Module 3
1. Module 3
1.36. Page 7
Module 3—Electrical Phenomena
Potential Difference

© Yury Asotov/shutterstock
Electronic technicians complete a number of tasks when assembling circuit boards. A voltmeter is frequently used when testing circuits. The word voltage stems from the fact that potential difference is measured in volts with a voltmeter.

© Ovidiu Iordachi/shutterstock
In these cases, the voltage is describing the amount of work required per unit of charge to move a test charge from one point to another within a circuit. Since the calculation involves subtracting one potential value from another, this quantity is called electric potential difference (or just potential difference for short).
electric potential difference: the change in electric potential experienced by a charge moving from one point to another in an electric field.
It is sometimes called potential difference.
In terms of an equation, electric potential difference is described as
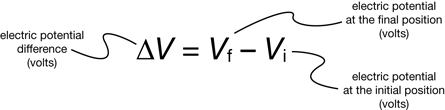
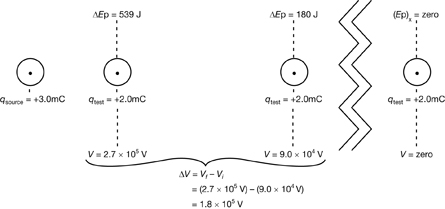
The following calculation shows how to calculate the electric potential difference if the test charge in the previous lab activity was moved from an initial location 300 m from the source to a final location 100 m from the source.
 Read
Read
You can find out more about voltage by reading the sections called “Electric Potential” and “Electric Potential Difference” on pages 563 to 566 of your textbook. Pay close attention to the explanation of the electron volt and to “Example 11.8.”
 Self-Check
Self-Check
SC 10.An electron is accelerated to high velocities within the picture tube of an old-style CRT (cathode ray tube) computer monitor. The potential difference used in the picture tube is 375 V.
- The charge of an electron is 1.60 × 10–19 C. Calculate the energy gained by the electron in joules.
- Calculate the energy gained by the electron in electron volts.
- Consider your answers to SC 10.a. and SC 10.b. Suggest a reason why the electron volt is considered to be a convenient unit for researchers studying the behaviour of electrons and other particles in electric fields.
SC 11. a. Complete “Practice Problem” 2 on page 566 of your textbook.
- Use your answer from SC 11.a. to determine the final velocity of the electron assuming that it started at 8.00×107 m/s. Remember that you can find the mass of the electron on your data sheet.
 Self-Check Answers
Self-Check Answers
SC 10.
Given
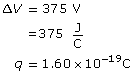
Required
The gain in energy of the electrons.
Analysis and Solution
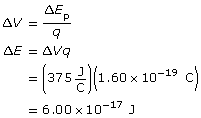
Paraphrase
The electrons gain 6.00×10−17 J.
Method 1
Given
The energy was calculated as Joules in SC 10.a.
ΔE = 6.00×10−17 J
1eV = 1.60×10−19 J
The conversion fraction is on the physics data sheet.
Required
The energy in electron volts.
Analysis and Solution
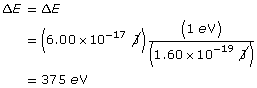
Paraphrase
The electron gains 375 eV.
Method 2
Given
ΔV = 375 V
q = 1e
Required
The energy in electron volts.
Analysis and Solution
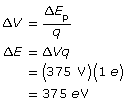
Note 1 e (1 elementary charge) is an exact value, therefore does not count for significant digits.
Paraphrase
The electron gains 375 eV.
The answer to the previous question labelled “Method 2” simply requires multiplying the value of the potential difference in volts by the charge of 1 electron. In this case, if an electron is accelerated through 375 V the energy gained is 375 eV. What could be easier?
SC 11.
Given
ΔV = 4.00×104 V
q = 1.60×10−19 C
Required
The energy of the electron in Joules and electron volts
Analysis and Solution
Since the electron has been accelerated by 4.00×104 V, the energy it has gained is 4.00×104 eV.
An energy value in Joules can be determined using the equation or by unit conversion.
Equation
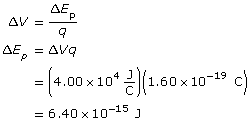
Unit Conversion
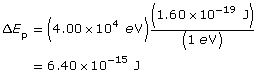
Paraphrase
The electron gains 4.00×104 eV or 6.40×10−15 J of energy.
Given
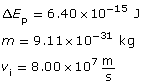
Required
The final velocity of the electron.
Analysis and Solution
Using the conservation of energy, the energy gained by the electron will be converted into kinetic energy.
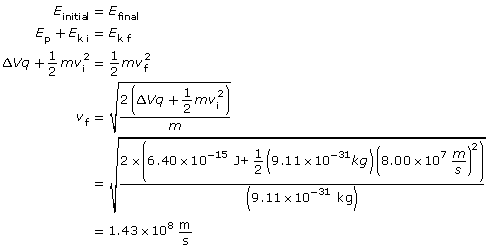
Paraphrase
The final velocity of the electron is 1.43×108 m/s.