1. Module 3

1.43. Page 3

Module 3 Lesson 6

Module 3—Electrical Phenomena

 

The Motion of Charged Particles in Uniform Electric Fields

 

A photo shows two people playing cricket.

© Forgis/2463953/fotolia

The motion of an individual charged particle in a uniform electric field is not something that most people observe on a daily basis. However, the motion of a mass in a uniform gravitational field is something that almost everyone has experienced but may not know it.

 

Think back to the last time you were watching or playing sports when a ball was given a velocity and then allowed to move through Earth's gravitational field. If the batter in the photo connects her bat with the ball, what additional information would you need in order to predict the motion of the ball?

 

If spinning effects can be ignored, the motion of the ball depends upon the direction of the initial velocity of the ball once it leaves the bat. As you'll see in the next question, the path of the ball is a consequence of Newton's laws of motion.

 

Self-Check

 

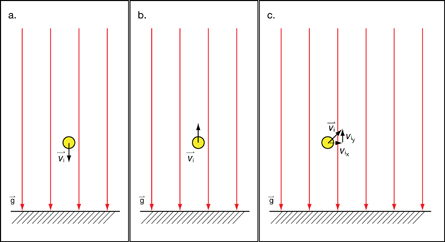
SC 5. In each of the following diagrams, the initial velocity of a softball is shown relative to the direction of the gravitational field. Make your own copy of each diagram, and add the following information:

  • the direction of the force of gravity on the ball
  • the path of the ball
  • the concise explanation of the path that you drew

Ignore the effects of air resistance, and consider the force of gravity to be the only force acting on the ball.

 

There are three illustrations. The illustration on the left shows the softball with an initial velocity straight down. The centre illustration shows the softball with an initial velocity straight up. The illustration on the right shows the softball with an initial velocity at an angle.

 

Check your work.
Self-Check Answers

 

SC 5.

 

The free-body diagram of the forces acting on the ball, showing that gravity is the only force acting on the ball.

 

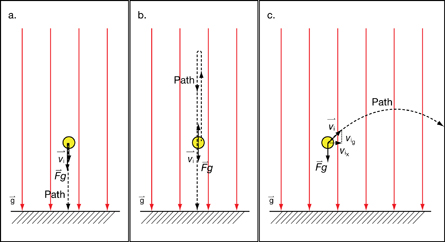
The diagram shows how the three balls move through the gravitational field. 1. The first ball goes straight down. 2. The second ball goes up, stops, and then comes straight down. 3. The third ball follows a parabolic path through the air.

The force of gravity is the only force acting on the ball, so it is an unbalanced force.

 

According to Newton's second law of motion, the ball will accelerate in the direction of the unbalanced force—straight down toward Earth's centre.

 

The downward acceleration is in the same direction as the initial velocity, so the ball speeds up as it travels on a path that takes it down—toward Earth’s centre.

The force of gravity is the only force acting on the ball, so it is an unbalanced force.

 

According to Newton's second law of motion, the ball will accelerate in the direction of the unbalanced force—straight down toward Earth's centre.

 

The downward acceleration is in the opposite direction as the initial velocity, so the ball initially slows down as it travels straight up, away from the centre of Earth. Eventually, the velocity of the ball reaches zero at its highest point. The ball continues to accelerate by speeding up as it travels straight down toward Earth’s centre.

The force of gravity is the only force acting on the ball so it is an unbalanced force.

 

According to Newton's second law of motion, the ball will accelerate in the direction of the unbalanced force—vertically down, toward Earth's centre.

 

Ignoring the effects of air resistance, in the horizontal direction there are no unbalanced forces acting on the ball. Newton's first law of motion states that in the absence of an external, unbalanced force, an object will maintain its velocity. Therefore, the ball moves with uniform motion in the horizontal direction. In other words, the downward acceleration due to gravity is perpendicular to the horizontal component of the ball's initial velocity, so the ball’s horizontal motion is unaffected by this acceleration.


The downward acceleration is in the opposite direction as the vertical component of the initial velocity, so the ball initially slows down as it travels straight up, away from the Earth’s centre. Eventually, the vertical component of the ball's velocity reaches zero at its highest point. The ball continues to accelerate in the vertical direction by speeding up as it travels straight down toward the Earth’s centre. The combination of uniform motion in the horizontal direction, with accelerated motion in the vertical direction, is a path that has the characteristic parabolic shape of projectile motion.

 

 
Read

 

You can learn how the motion of charged particles can be analyzed in uniform electric fields by reading pages 572 and 573 of your textbook. Note how kinetic and potential energy are assigned zero values in “Example Problem 11.11.”

 

Self-Check

 

SC 6. Solve “Practice Problem” 1 on page 573 of your textbook.

 

Check your work.
Self-Check Answers

 

SC 6.

 

Given

 

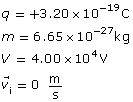
An alpha particle is released beside the positive plate in a parallel plate apparatus. When released the particle has no kinetic energy but has a potential energy equal to qV. When the particle strikes the negative plate, it no longer has potential energy it has all changed into kinetic energy mv2/2.


 

Required
 

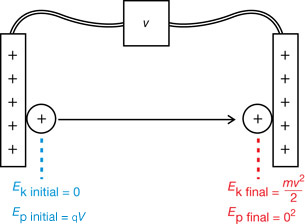
The final speed of the alpha particle, the instant before hitting the negative plate.

 

Analysis and Solution

 

In terms of electric potential energy, if the electric potential energy at the negative plate is zero, then the electric potential energy of the system at the positive plate is E = qV. In terms of kinetic energy, the alpha particle is at rest at the positive plate so the kinetic energy at that location is zero. Just before striking the negative plate the kinetic energy of the alpha particle is ½mv−2final.

 

 

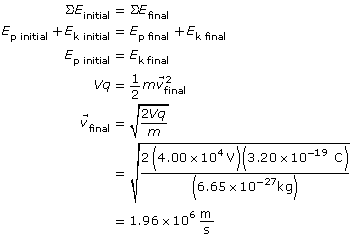
Paraphrase

 

The final speed of the alpha particle is 1.96×106 m/s.

 

 

The same physics principles used to analyze the motion of a softball in the gravitational field of Earth can be used to analyze the motion of a charged particle moving in a uniform electric field. When a charge travels through a uniform electric field, the type of motion that results depends on the direction of the force acting on the particle relative to the direction of the particle's initial velocity. In the next lab activity you will have an opportunity to investigate this further.