1. Module 4

1.12. Page 4

Lesson 2

Module 4—Magnetic and Electric Fields in Nature and Technology

 
Read

 

Refer to pages 598−600 of the textbook for an explanation of how to calculate the magnetic force acting on a charged particle.

 

Self-Check

 

Experiments were conducted to see if flue gases from a power plant could be cleaned using a magnetic field. In one experiment with particles of mass 2.0 × 10–20 kg, and speed of 1.50 × 10–2 m/s, the following data was collected:

 

Charge on Particle (×10–17 c)

Radius of Curvature (×10–3 m)

1

150

2

75

3

50

4

36

5

30

10

15

 

Use the data to answer the following questions.

 

SC 1. Graph the data and draw a best-fit curve through the data points.

 

SC 2. Is there an easy way for you to find the magnetic field strength from this information?

 

SC 3. Graph the data using the reciprocal of the charge in place of the charge and draw a best-fit curve through these data points.

 

SC 4. Is there an easy way for you to find the magnetic field strength from this new graph?

 

Check your work.
Self-Check Answers

 

Contact your teacher if your answers vary significantly from the answers provided here.

 

SC 1. You can graph the data in several ways. You might

  • use graph paper and plot the points by hand

  • use a graphing calculator to graph the points

  • use a spreadsheet to graph the points

This graph uses a spreadsheet to graph the points. You may think of better titles for the graph and labels for the axes when you create your own graphs.

 

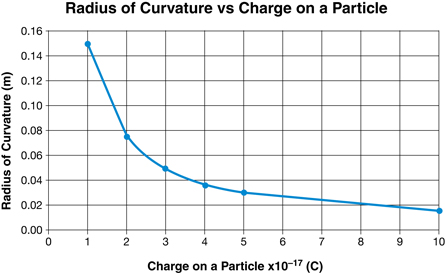
A graph of the radius of curvature versus charge on a particle. The graph shows an inverse relationship with a curved line going down to the right.

 

SC 2. With a curved graph, it is difficult to find the magnetic field strength.

 

SC 3. Again, the data can be graphed in several ways. This graph uses a spreadsheet to graph the points. You may think of better titles for the graph and labels for the axes when you create your own graphs.

 

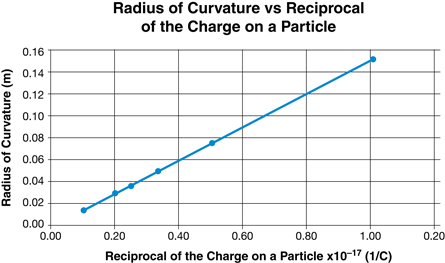
A graph of the radius of curvature versus the reciprocal of the charge on a particle. The graph shows a proportional relationship with a straight line going up to the right.

 

SC 4. This graph is a straight line. The slope of this graph gives an easy way to find the magnetic field strength. The slope is equivalent to , so the magnetic field strength can be found from .

 

In this self-check question you used curve straightening to get useful information. You should consider using this technique whenever you need more information from a curved graph.

 

The Direction of the Magnetic Force

 

As you discovered earlier, the magnetic force causes the charged particle to travel in uniform circular motion.

 

Module 4: Lesson 2 Assignment

 

Remember to submit the answers to A 1 to your teacher as part of your Module 4: Lesson 2 Assignment.

 

A 1. As a review, draw the inward force on the following diagrams. The first one has been completed as an example.

 

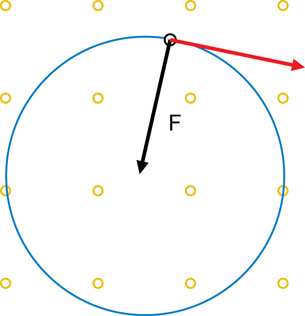
a. The circular motion of a negative charge is shown moving clockwise in a magnetic field pointing out of the page. A force points from the particle to the centre of the circular motion.
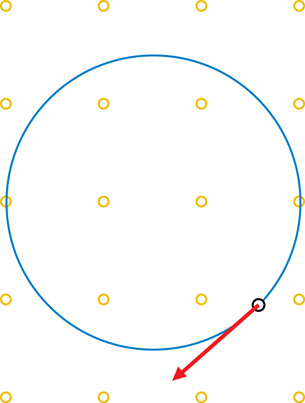
b. The circular motion of a negative charge is shown moving clockwise in a magnetic field pointing out of the page. Draw in the correct force.


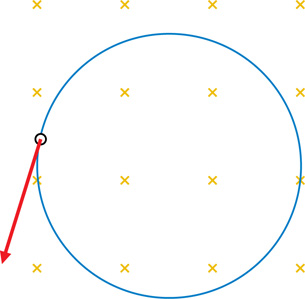
c.The circular motion of a negative charge is shown moving counter-clockwise in a magnetic field pointing into the page. Draw in the correct force.


 

When a charged particle is moving at right angles to a magnetic field, the force exerted on the particle by the field is perpendicular to both the particle's velocity and the magnetic field. Refer again to the diagram on page 594 of the textbook. It may help to think of it this way: two of the quantities will be in the same plane of motion (able to be drawn on the same piece of paper) and the third will be into or out of that plane (the piece of paper).

 

To predict the direction of the magnetic force, one only needs to know the direction of the particle's velocity and the direction of the magnetic field. However, this does not completely define the direction of the force. There is still an ambiguity because a perpendicular has two directions. This ambiguity is resolved by the left-hand rule illustrated in Figure 2. (There are several hand rules for this purpose. The following is only one suggestion.)

 

Left-hand Rule for Deflection: The direction of the force exerted on a negatively charged particle moving in a magnetic field can be visualized by the left-hand rule.

 

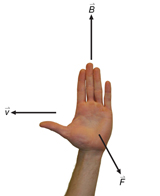
An illustration shows the left-hand rule. The view shows the hand held vertically with the palm facing the viewer, thumb pointing left, and fingers pointing straight up. The thumb points in the direction of the electron, the fingers point in the direction of the magnetic field, and the palm points in the direction of the magnetic force.

 

Figure 2

 

Hold your left hand flat with outstretched fingers in the direction of the magnetic field () and with the thumb pointing off to one side in the direction of the particle's velocity (). The palm of your hand will then be pointing in the direction of the magnetic force ().

 

This left-hand rule predicts the force that would act on negative charge. For a positive charge, use your right hand with your fingers, thumb, and palm representing the same quantities.


 

Example Problem 1.

 

A negatively charged particle is travelling right in a magnetic field that is directed downward.

  1. Is the magnetic force “out of” or “into” the plane of the page?

  2. If the particle where positively charged, in what direction would the magnetic force point?

Solution

 

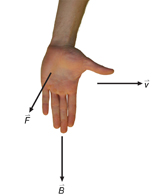
An illustration shows the applied left-hand rule. The view shows the hand held vertically with the palm facing the viewer, thumb pointing right, and fingers pointing straight down. The thumb points to the right in the direction of the electron, the fingers point downwards in the direction of the magnetic field and the palm points out of the page in the direction of the magnetic force.

  1. According to the left-hand rule, the force is directed “out of” the plane of the page.

  2. For a positive charge, using your right hand, the force would be “into” the plane of the page.

Example Problem 2.

 

A positively charged particle is travelling left in a magnetic field that is directed downward.

  1. Is the magnetic force “out of” or “into” the plane of the page?

  2. If the particle where negatively charged, in what direction would the magnetic force point?

Solution

 

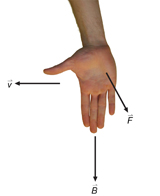
An illustration shows the applied right-hand rule. The view shows the hand held vertically with the palm facing the viewer, thumb pointing left, and fingers pointing straight down. The thumb points to the left in the direction of the positive charge, the fingers point downwards in the direction of the magnetic field and the palm points out of the page in the direction of the magnetic force.

  1. According to the right-hand rule, the force is directed “out of” the plane of the page.

  2. For a negative charge, using your left hand, the force would be “into” the plane of the page.

Module 4: Lesson 2 Assignment

 

Remember to submit the answers to A 2 to your teacher as part of your Module 4: Lesson 2 Assignment.

 

A 2. Predict, draw, and verify the magnetic force on each diagram below. Verify your answers using the simulation.

 

a. positive charge

A positive particle is shown moving to the right in a magnetic field that is out of the page.

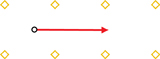
b. positive charge

A positive particle is shown moving to the right in a magnetic field that is into the page.

c. negative charge

A negative particle is shown moving to the right in a magnetic field that is into the page.

d. negative charge

A negative particle is shown moving to the right in a magnetic field that is out of the page.


 

A combination of both equation (4) and the appropriate hand rule can be used to determine the magnitude and direction of the magnetic force acting on a moving charged particle. You will need to refer to your physics data sheet for the charge of an electron, proton, and alpha particle. Note the definition of the following terms that apply to the practice problems that follow:

  • “upward” means “out of” the plane of the page () (not to be confused with the term “north”)

  • “downward” means “into” the plane of the page () (not to be confused with the term “south”)

Example Problem 3.

 

Calculate the magnitude and direction of the magnetic force acting on a proton travelling north at a speed of 2.75 × 103 m/s through magnetic field of 3.50 × 10–1 T that is directed west.

 

Magnitude

 

Fm = qvB

Fm = (1.60 × 10–19 C)(2.75 × 103 m/s)(3.50 × 10–1 T)

Fm = 1.54 × 10–16 N

 

Direction

 

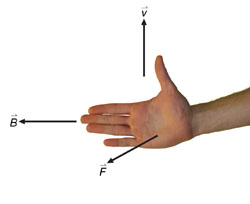
An illustration shows the application of the right-hand rule. The view shows the hand held horizontally with the palm facing the viewer, thumb pointing up, and fingers pointing to the left. The thumb points north in the direction of the positive charge. The fingers point west in the direction of the magnetic field and the palm points upward in the direction of the magnetic force.

 

According to the right-hand rule for positive charges, the force is upward.

 

Self-Check

 

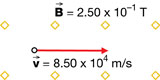
SC 5. Based on the following diagram, predict the magnitude and direction of the magnetic force acting on each proton. You can only verify the direction using the simulation.

 

a. An illustration shows a proton moving towards the right at 8.50 times 10 exponent 4 m/s. The magnetic field is upward with a strength of 2.50 times 10 exponent minus 1 T.
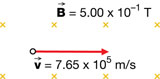
b. An illustration shows a proton moving towards the right at 7.65 times 10 exponent 5 m/s. The magnetic field is downward with a strength of 5.00 times 10 exponent minus 1 T.
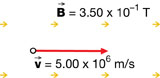
c. An illustration shows a proton moving towards the right at 5.00 times 10 exponent 6 m/s. The magnetic field is west with a strength of 3.50 times 10 exponent minus 1 T.


 

Check your work.
Self-Check Answers

 

SC 5.

 

a. An illustration shows a proton moving towards the right at 8.50 times 10 exponent 4 m/. The magnetic field is upward with a strength of 2.50 times 10 exponent minus 1 T.

 

direction: south

 

Fm = qvB

Fm = (1.60 × 10–19 C)(8.50 × 104 m/s)(2.50 × 10–1 T)

Fm = 3.40 × 10–15 N

 

b. 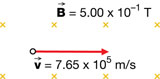An illustration shows a proton moving towards the right at 7.65 times 10 exponent 5 m/s. The magnetic field is downward with a strength of 5.00 times 10 exponent minus 1 T.

 

direction: north

 

Fm = qvB

Fm = (1.60 × 10–19 C)(7.65 × 105 m/s)(5.00 × 10–1 T)

Fm = 6.12 × 10–14 N

 

c. 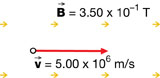An illustration shows a proton moving towards the right at 5.00 times 10 exponent 6 m/s. The magnetic field is west with a strength of 3.50 times 10 exponent minus 1 T.

 

Direction: none

 

magnitude: none −the motion and field direction are parallel.