Module 5
1. Module 5
1.9. Page 2
Module 5—Wave Theory of Light
 Explore
Explore

Physics (Pearson Education Canada, 2007) p. 648, fig 13.21. Reproduced with permission.
Olaus Roemer (1664–1710) and Christiaan Huygens made one of the earliest attempts to measure the speed of light using astronomical data. The period of revolution for Jupiter’s moon, Io, was well known. It would periodically disappear from sight, or eclipse, as it travelled behind Jupiter only to reappear on the other side every 42.5 hours.
However, depending on the time of year you observed the eclipse, it would appear 22 minutes behind schedule. Presumably, this time difference is caused by the extra distance the light has to travel when Jupiter and Earth are on opposite sides of the Sun. Given that the extra distance is equal to Earth’s orbital diameter and the time it takes to travel that distance, Roemer was able to measure the speed of light to be 2.3 × 108 m/s. And although it was very close to the currently accepted value of 3.0 × 108 m/s, this figure was rejected by the scientific community of the time, who assumed it to be much too high a figure because no such speed even remotely near had ever been measured.
 Self-Check
Self-Check
SC 1. The radius of Earth’s orbit is 1.49 × 1011 m. If the eclipse of Io took 22 minutes longer, demonstrate the calculations Roemer and Huygens used to calculate the speed of light.
SC 2. The value that Roemer and Huygens measured was considered much too large. In the 1700s, what was considered really fast?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Given

Required
the speed of light
Analysis and Solution
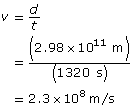
Paraphrase
Roemer and Huygens determined the value was 2.3 × 108 m/s.
SC 2. In the 1700s the fastest form of transportation was a horse, with a top speed of approximately 70 kph or 20 m/s. Even the fastest animal, a cheetah, had a maximum speed of only approximately 27 m/s. William Derham (1657–1735) was the first person to measure the speed of sound as 3.4 × 102 m/s. The speed of light measured at 3.0 × 108 m/s, which was about a million times faster than sound and was fast beyond imagination.
Even today, the space shuttle, the fastest human vehicle ever, has a maximum speed of 7800 m/s, which is approximately 0.0026% or twenty-six ten-thousandths of one percent of the speed of light.
 Read
Read
In 1848, the first terrestrial attempt to measure the speed of light was done by Armand Fizeau using a toothed wheel. See his experimental design on page 649 of your textbook.
 Self-Check
Self-Check
SC 3. What was the manipulated variable in Fizeau’s experiment?
SC 4. What was the responding variable in Fizeau’s experiment?
SC 5. What did Fizeau see during his first experiment?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3. The manipulated variable in Fizeau’s experiment was the speed at which the toothed wheel turned. This is also called the wheel’s frequency of rotation.
SC 4. The responding variable in Fizeau’s experiment was whether or not the observer could see the light.
SC 5. In the first experiment, Fizeau would see the light reflected from the mirror. As the toothed wheel spun faster, the tooth would start to block the reflected light source so Fizeau would not be able to see the reflected light source. As the wheel continued to speed up, the light source would again become visible as the tooth would move all the way through the path of the light before the reflected light reached the toothed wheel.

Physics (Pearson Education Canada, 2007) p650, fig 13.24. Reproduced with permission.
Michelson Experiment
In 1905, Albert Michelson accurately measured the speed of light using a set of rotating mirrors. In his now-famous experiment, light was directed at an eight-sided, rotating mirror. The light was reflected from one side of the rotating mirror toward a distant curved mirror that sent the light back toward the rotating mirror. If the rotating mirror completed one-eighth of a rotation (or a multiple of 1/8) by the time the light returned, the light would be reflected to an observer (as seen in the illustration). Knowing the period of rotation that causes the light to be observed gives the time it takes the light to travel to and from the distant curved mirror. Therefore, the speed of light was equal to the distance to and from the curved mirror divided by 1/8 of the period of rotation.
 Read
Read
Read “Michelson’s Experiment” and “Example 13.1” on pages 650 and 651 of your textbook.
 Try This
Try This
TR 1. Complete “Practice Problems” 1–3 on page 650 of your textbook. Try question 3 first.
TR 2. Now that you have read about several methods scientists have used to measure the speed of light, design a procedure for your own experiment to measure the speed of light.
 Module 5: Lesson 2 Assignment
Module 5: Lesson 2 Assignment
Remember to submit your answer to A 1 to your teacher as part of your Module 5: Lesson 2 Assignment.
A 1. Do Application questions 4, 7, 8, and 10 on page 652 of your textbook.
 LAB: Determining the Speed of Light Using a Microwave Oven
LAB: Determining the Speed of Light Using a Microwave Oven

© trailexplorers/shutterstock
Retrieve your copy of the Module 5: Lesson 2 Assignment you saved earlier in this lesson. Before performing this lab, read “Quicklab” on page 651 of your textbook. Perform the procedure that follows.
Problem
How can a microwave oven be used to determine the speed of light?
Materials
- microwave oven
- microwave-safe dish, such as a casserole dish
- marshmallows
Procedure
- Place a layer of marshmallows in a microwave-safe dish or casserole dish, ensuring the marshmallows cover the bottom of the dish with no empty spaces between the marshmallows.
- Remove the turntable from the microwave oven.
- Place the dish in the centre of the microwave, and cook on high power until you see the marshmallows begin to melt in various locations.
- Remove the dish from the oven and let it cool.
- Measure the distance between adjacent melted spots from centre to centre. This distance is one-half the wavelength of the microwave.
- Calculate the average distance of separation for all the spots.
- Calculate the wavelength by multiplying the average separation distance by two.
- Record the frequency of the microwave oven, which is listed on the door or back of the microwave or in its documentation.
Observations
Record the distance of separation between adjacent melted spots (measured centre to centre) in a table like this one. If you do not have access to a microwave, use the values in the table.
Measurement Number |
Distance of Separation (cm) |
1 |
approx. 6.0 |
2 |
approx. 6.0 |
3 |
approx. 6.0 |
4 |
approx. 6.0 |
microwave frequency = 2.5 × 109 Hz
 Module 5: Lesson 2 Assignment
Module 5: Lesson 2 Assignment
Remember to submit your answers to LAB 1, LAB 2, LAB 3, LAB 4, LAB 5, LAB 6, and LAB 7 to your teacher as part of your Module 5: Lesson 2 Assignment.
Analysis
LAB 1. Calculate the average distance of separation for at least four measurements.
LAB 2. Convert the average distance from centimetres to metres.
LAB 3. Determine the microwave wavelength.
LAB 4. Calculate the speed of light in metres per second using the microwave’s frequency and wavelength according to the universal wave equation (c = fλ).
Conclusions
LAB 5. According to your observations, at what speed do microwaves travel?
LAB 6. Determine the percentage of error when your measured speed is compared to the currently accepted speed of 3.00 × 108 m/s.
![]()
LAB 7. Why is the prefix “micro” used to describe “microwaves”?
 Discuss
Discuss

© Sergey Popov V/shutterstock
Do light and all other classifications of EMR always travel at 3.00 × 108 m/s? This common value gives the speed of light when it travels in a vacuum or in air. But what happens to the speed of light when it enters water or a glass? Does the speed slow down, speed up, or stay the same? Can it be stopped? Furthermore, if the medium, such as water, in which light travels is moving, can light travel faster than 3.00 × 108 m/s?
D 1. See Fizeau’s apparatus on page 649 of your textbook. How did Fizeau’s water experiment support the wave model of light? Post an explanation to the discussion questions to the discussion area for your class.