Module 5
1. Module 5
1.21. Page 4
Module 5—Wave Theory of Light
 Read
Read
Read “Total Internal Reflection” on pages 672–673 of your textbook for more information on critical angles.
 Try This
Try This
TR 5. Manipulate Snell’s Law to give an expression that will solve for the critical angle:
![]()
TR 6. Calculate the critical angle for water. Is this critical angle supported by the data collected in Table 3? Verify your answer using the Light Refraction simulation.
Applications of Total Internal Reflection: Light Pipes and Mirages
Light pipes (and fibre optics) are very common in medicine, science, and industry. They work by trapping light using total internal reflection. You can easily produce a light pipe using a long Lucite rod. Lucite is a common type of plastic that has a relatively high index of refraction at 1.49.
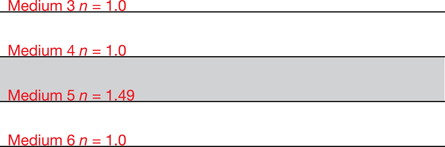
SIM 1. Use the Light Refraction simulation to build a light pipe similar to that shown here. Position the laser pointer in the Lucite layer (n = 1.49) and point it so that total internal reflection occurs. Explain how it traps the light.
SIM 2. Suppose you submerged your Lucite light pipe in water. Would that improve or degrade the performance of your light pipe? Explain.

© vera bogaerts/shutterstock
An old joke says, "Is that a mirage or am I seeing things?" In fact, a mirage is not an optical illusion. You really are seeing something when you see a mirage. One of the most common mirages is the wet appearance of a prairie road or field on a hot summer day. This happens because the air layer above the ground is very hot and has a slightly lower refractive index than the cooler air just above it. Such a refractive index gradient is illustrated by the following ray diagram and observed in the photo on the right.
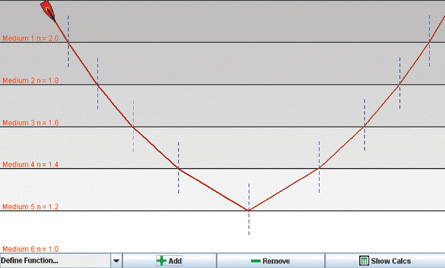
SIM 3. Mirage conditions can be set up in the Light refraction simulation. Use the laser pointer as the Sun and set up multiple layers with the upper layer having the highest index of refraction and the lower ones with progressively smaller indexes of refraction. Can you produce a mirage? What are you seeing when you think you are seeing water on the road? Sketch how this mirage is formed. Why do you see a mirage? See “Figure 13.45” on page 667 of your textbook.
The Refraction of White Light in a Prism: Dispersion
Triangular prisms can be used to separate white light in its spectral components (colours). This occurs because the angle of refraction depends on the index of refraction, which is unique for each wavelength.
Recall that in the expanded form of Snell’s Law, the wavelength and index of refraction are related to one another as follows:
![]()
When any light wave enters the prism from the air, its wavelength is compressed as it slows down. And since the refractive index of air (n1) is equal to 1.0, the ratio of the wavelength before and after the refraction determines the refractive index of the medium for each wavelength.
![]()
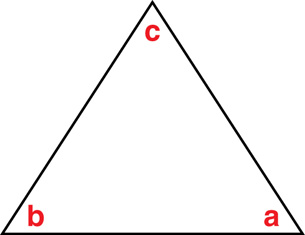
Recall the basic properties of all triangles:
- The sum of the interior angles in a triangle is 180°. According to the noted triangle, a + b + c = 180°.
- The complimentary angles are angles that add to form a 90° angle or right angle.
- The supplementary angles are angles that add to form a 180° angle or a straight angle.
 Try This
Try This
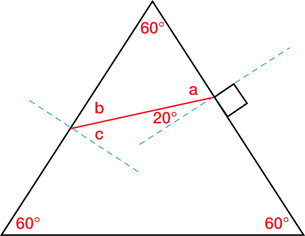
TR 7. In the diagram on the left, the blue dashed lines represent surface normals to the triangle. These lines form 90° angles with the respective faces they pass through. Explain how you know that angle a = 70°.
TR 8. Determine angle b if angle a is 70°.
TR 9. Knowing angle b, determine angle c.
Tracing a Ray Through a Prism to Verify Dispersion
A simulation will be used to verify ray diagrams and calculations that demonstrate that different colours of light will be separated as they pass through a prism. Open the Prism simulation and select “One Prism” to complete the following activities. Note that each prism in the simulation is an equilateral prism with 60° angles at each corner.
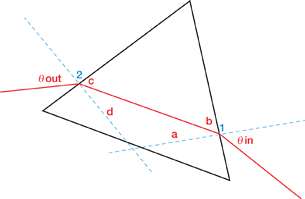
SIM 4. Set the refractive index of the prism to n = 1.55, and rotate the prism to an angle of 100° as shown in the diagram on the right. This will make the incident angle for the ray entering the prism θin = 43.68°.
- Using Snell’s Law and the refractive index of air (n = 1.00), show the calculations for determining angle a. Verify your answer by pressing “Show Calcs” (
 ).
).
- Using the techniques developed in recent Try This activities and the fact that the prism is an equilateral triangle, calculate the angles b, c, d, and θout. Verify your final answer on the simulation by pressing “Show Calcs” (
 ).
).
 Module 5: Lesson 4 Assignment
Module 5: Lesson 4 Assignment
Remember to submit your answer to LAB 7 to your teacher as part of your Module 5: Lesson 4 Assignment.
LAB 7. Consider white light entering an equilateral prism at a 50° angle with respect to the normal of one of its faces. If the index of refraction is 1.66 for blue light and 1.62 for red light, how far apart, in degrees, will the two rays emerge? Trace the path of the blue and red light on each of these prisms. Sketch and label all angles, and determine the angular separation between the blue and red rays as they leave the prism. Use the Prism simulation to verify your answer.



© 2009 Jupiterimages Corporation
 Read
Read
Read “Prisms—Dispersion of White Light” on pages 675–676 of your textbook for more information on the composition of white light.