Module 6
1. Module 6
1.4. Page 2
Module 6—Wave-Particle Duality and Quantum Physics
 Explore
Explore
Blackbody Radiation
In 1862 German physicist Gustav Kirchhoff introduced the term blackbody to describe a hypothetical object that absorbs all of the electromagnetic radiation (EMR) that falls on it. In theory, the energy of all the absorbed EMR causes the blackbody to heat up and become a perfect radiator, emitting energy back to the environment in the form of EMR. Some of the EMR can be seen in red- or white-hot objects and longer wavelengths can be felt as heat. The heating element on a stove can be considered a blackbody radiator—you can feel the infrared EMR and see the visible EMR at sufficient temperatures.
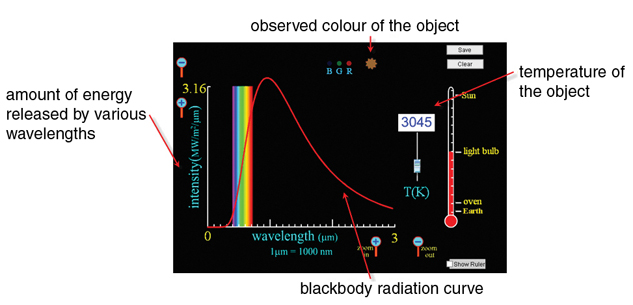
The relationship between temperature and colour can be summarized using a Blackbody Spectrum simulation. Open the simulation and see what happens when you adjust the temperature using the slider.
blackbody radiation curve: a graph of the intensity of EMR versus wavelength for an object at a given temperature
incandescent: glowing with heat
As illustrated below, the simulation shows the observed colour of an object at the temperature indicated on the slider. In this example, a blackbody radiation curve shows the distribution of energy by wavelengths released by an incandescent light bulb when it is 3045 Kelvin (2772°C). Notice that the bulb emits most of its energy in wavelengths slightly larger than those of visible light, which is infrared heat. Interestingly, this is why an incandescent light bulb is very inefficient at producing light—90% of the energy it consumes produces infrared heat rather than visible light!
One interesting thing about blackbody radiation curves is that you can use an object’s curve, along with its observed colour, to tell the object’s temperature!
© The University of Colorado, under the GNU General Public License (GPL)
 Try This
Try This
TR 1. Using the Blackbody Spectrum simulation, complete the third relationship between colour and temperature.
- Extremely hot, glowing objects, such as stars, emit a continuous range of wavelengths, making them appear white.
- At a given temperature, the energy emitted by a hot object comprises a specific range of wavelengths, giving it a unique colour.
- At _______ temperatures, an object emits more blue light; at _______ temperatures, it emits more red light.
 Self-Check
Self-Check
SC 1. Using the radiation curves in the simulation, explain why a light bulb appears white while an oven element only has a slight red glow. What does this imply about the temperature of the filament in a light bulb compared to that of an element in a stove?
 Self-Check Answer
Self-Check Answer
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Light Bulb
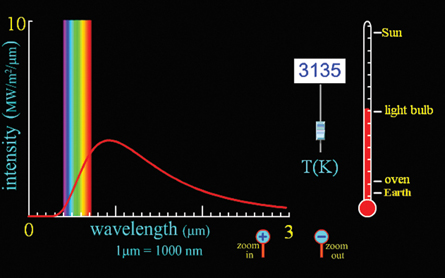
The bulb appears white because it emits some energy in wavelengths that span across the visible range of wavelengths. The longer, infrared wavelengths are not seen but are felt as heat.
Stove Element
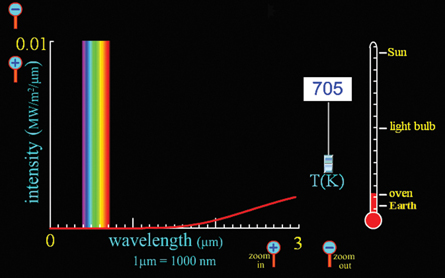
Zooming in several times along the intensity axis reveals that oven temperatures release energy with wavelengths that approach the red end of the visible spectrum. The element in an oven will start to appear red when it reaches temperatures near 1300 K. (Note the inside of an oven is much cooler than this, which is why the element cycles on and off and the entire oven does not glow red hot.) You can adjust the temperature on the simulation upward to find the exact temperature at which red light will start to appear.
The temperature of the filament in a light bulb is much higher than that of a stove element, even during the heating cycle.
 Read
Read
Read pages 704 and 705 of the textbook for more information on blackbody radiation and curves. Note that some of the radiation curves shown in the text are related to frequency rather than to wavelength, as seen in the simulation.
The Quantum
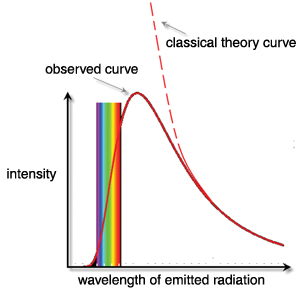
The explanation for blackbody radiation and, in particular, the shape of the radiation curves, could not be found in classical physics. For example, classical physics predicts that as an object heats up it should start releasing energy in shorter and shorter wavelengths, since this is the most efficient way to release energy. At very high temperatures, the amount of energy released is maximized by the release of ever-shorter wavelengths.
quantum (pl. quanta): the smallest bundle or packet of energy that a given wavelength or frequency of EMR can possess
Planck’s formula: EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation,
However, the blackbody radiation curves produced by hot objects show that even at extremely high temperatures, most of the energy is released by relatively long wavelengths with little or no energy released by very short wavelengths. The explanation for the shape of the observed curves came from Max Planck in the year 1900. He could account for the shape by assuming that there was a specific amount of energy that any given wavelength of radiation could exchange with its environment. The term quantum refers to this specific energy, and it is related to the wavelength of the radiation by Planck’s formula.
Planck’s EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation |
|||||||||||||||
|
|||||||||||||||
* n refers to the whole number of quanta that make up the total amount of energy (E) transferred by the radiation; therefore, n = 1, 2, 3, 4, . . . . |
|||||||||||||||
Note that Planck’s formula applies equally to wavelength as it is related to frequency by the universal wave equation.
|
Planck’s formula represents a fundamental shift in theory. In this system the amount of energy that can be exchanged between radiation and its surroundings is quantized, or limited to whole-number multiples of the smallest unit of energy—the quantum. Furthermore, the value of each quantum is equal to the product of Planck’s constant and the frequency of the radiation (E = hf). The concept of the quantum effectively ended classical physics and gave birth to quantum physics.
photon: one quantum of light
 Read
Read
Read “Einstein, Quanta, and the Photon” on page 706 of the textbook.
 Try This
Try This
TR 2. Complete “Practice Problems” 1, 2, and 3 on page 706 of the textbook.
TR 3. Complete “Practice Problems” 1, 2, and 3 on page 707 of the textbook.
TR 4. Complete “Practice Problems” 1 and 2 on page 708 of the textbook.
Energy and the Spectrum
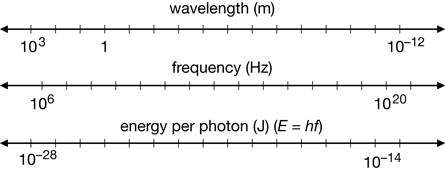
Planck’s formula associates photon energy with the frequency of radiation, expanding the electromagnetic spectrum to show the energy of various classifications of EMR.
 Module 6: Lesson 1 Assignment
Module 6: Lesson 1 Assignment
Remember to submit your answers to A 1, A 2, A 3, A 4, A 5, A 6, A 7, and D 3 to your teacher as part of your Module 6: Lesson 1 Assignment.
A 1. Why couldn’t classical physics explain blackbody radiation curves?
A 2. What is the frequency of a 13.0-eV photon?
A 3. What is the wavelength of a 4.30×10–19-J photon?
A 4. How many photons with a wavelength of 532 nm are released each second by a 5.0-mW laser?
A 5. As a safety precaution when working with lasers, scientists wear red-coloured glasses that will block all colours but red. Why is a red laser safer than a blue laser?
A 6. A person lives near a 50-kW radio tower. Why is it safe to live near the high-power radio tower but dangerous to be exposed to an X-ray machine that uses 7.5 kW?
A 7. Why did the introduction of the photon effectively end classical physics? What does this mean for the Christiaan Huygens theory that light is a series of waves and Thomas Young’s double-slit experiment?
 Discuss
Discuss
D 1. Develop a mnemonic that will help you remember the order of radiation given in “Figure 14.6” on page 709 of the textbook. RMIVUXG = Radio Microwave Infrared Visible Ultraviolet X-ray Gamma. Post your mnemonic in the discussion area for your class.

© cloki/shutterstock
D 2. Using the concepts of quanta and photons, explain the difference between a 100-W and 40-W light bulb if they both produce only green light. Post your answers in the discussion area for the following questions:
- Why does the 100-W bulb appear brighter than the 40-W bulb?
- Why would you expect the 100-W bulb to feel hotter than the 40-W bulb?
- If 10% of the energy consumed by the bulb produces green light of 500 nm, how many green photons does each bulb produce each second? How does this support your explanation of brightness?
D 3. Read the answers from two other students for D 2 and improve your own answer. Explain what you learned from reading the other students’ answers and if or how you changed your own solution.
Discussion Scoring Guide
Principles involved: energy of a photon and power |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. | Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. | Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. | Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. | The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. | The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. | The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable. |