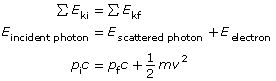Module 6

Module 6—Wave-Particle Duality and Quantum Physics

 

Explore

 

The Compton Effect

 

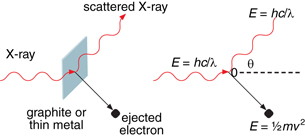
Einstein’s photon model of the photoelectric effect suggested that a photon behaves as a particle. Other experimental observations also supported the idea that a photon behaves as a particle. While experimenting with X-rays directed at graphite blocks, Arthur Compton observed what is now known as the Compton effect. He noticed that when X-rays are scattered by a graphite block, there is a subtle change in their wavelength and that this change is related to the angle at which the X-rays are scattered. The scattering of an X-ray when it collides with an electron is now known as Compton scattering.

 

Compton observed the energy and momentum of the incident X-ray, the scattered X-ray, and the electron and discovered that the collision demonstrated the conservation of momentum and energy—just as it would for an elastic collision between two particles. The experimental design is similar to that of a photoelectric effect, except using X-rays rather than lower energy EMR.

 

 

In terms of energy, Compton found that the total energy of the incident X-ray and the electron before the collision were equal to the total energy of the scattered X-ray and the ejected electron after the collision. This shows that the collision that occurred is perfectly elastic.

 

In terms of momentum, it is possible to generate an expression for the momentum of a wave using Einstein’s equation . Accordingly, mass and energy are just different forms of the same thing.

 

Manipulating the equation in terms of mass gives .

 

The familiar momentum equation can also be expressed in terms of mass: .

 

Putting the two equations together gives , since v = c for a photon travelling at the speed of light.

 

Substituting produces the following two equations that describe the momentum of a photon: .

 

By measuring the wavelengths of the incident and scattered X-rays as well as the velocity of the ejected electron, Compton was able to analyze the momentum involved in the collision between a photon and an electron. He determined that the total momentum of the incident X-ray photon was equal to the total momentum of the scattered X-ray photon and the ejected electron. Indeed, the collision appears to behave as a perfectly elastic collision between two particles.

 

Self-Check

 

SC 1. Complete the “Concept Check” on page 721 of your physics textbook.

 

SC 2. Draw a vector addition diagram to show the conservation of momentum applied to the Compton effect shown in the diagram above.

 

 

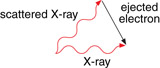
The Compton Equation

 

As noted above, the change in wavelength of the incident photon varies depending on the scattered angle. Using algebra and Einstein’s theory of relativity, the Compton scattering can be analyzed mathematically with the following equation.

 

The change in wavelength of the X-ray before and after the collision is related to the angle at which it scatters.

Note: change in wavelength ∆λ = λf – λi Quantity Symbol SI Unit wavelength λ m Planck’s constant h 6.63 × 10–34 J•s mass of an electron m 9.11 × 10–31 kg scattering angle—the angle between the incident ray and the scattered ray θ degrees

 

Watch and Listen

 

Open Compton Effect to see a demonstration of Compton's work.

 

Read

 

Read “The Compton Effect” on pages 721–725 of your physics textbook.

 

Try This

 

TR 1. Complete “Practice Problems” 1 and 2 on page 723 of your physics textbook.

 

TR 2. Complete “Practice Problem” 1 on page 724 of your physics textbook.

 

Energy of a Photon

 

So far you've been working with two forms of the equation to find a photon’s energy: and . By rearranging the momentum formula above, you now have a third equation for a photon’s energy: , where p is the momentum of the photon in kg•m/s and c is the speed of light in a vacuum.

 

Conservation of Energy

 

The collision observed in Compton’s experiment is perfectly elastic, so the kinetic energy is conserved.

 

Recall: Most collisions observed in real life are not perfectly elastic. In these collisions some of the initial kinetic energy is transformed into other forms, such as heat and sound. In collisions that are not perfectly elastic, Ek final < Ek initial.

 

The kinetic energy of the incident X-ray photon is equal to the kinetic energy of the scattered X-ray photon plus that of the recoil electron.

Quantity Symbol SI Unit momentum P kg•m/s speed of light in a vacuum c 3.00 × 108 m/s mass of an electron m 9.11 × 10–31 kg velocity of the recoil electron v m/s

 

Try This

 

TR 3. Complete “Practice Problem” 3 on page 723 of your physics textbook.

 

Module 6: Lesson 3 Assignment

 

Remember to submit your answers to A 1, A 2, A 3, and A 4 to your teacher as part of your Module 6: Lesson 3 Assignment.

 

A 1. What is the difference between the photoelectric effect and the Compton effect?

 

A 2. How does the Compton effect show the wave-particle duality of light?

 

A 3. An X-ray with a frequency of 3.74 × 1020 Hz is incident on a thin piece of metal. The lower frequency X-ray on the other side is observed deflected at 48°. What is the frequency of the deflected X-ray?

 

A 4. The scientist changes the frequency of the incident X-ray to 4.50 × 1020 Hz and measures the deflected X-ray frequency of 4.32 × 1020 Hz. What is the angle of deflection?

 

Physics 30 Learn EveryWare © 2009 Alberta Education