Module 6
1. Module 6
1.14. Page 3
Module 6—Wave-Particle Duality and Quantum Physics
De Broglie’s Wave Equation
The photoelectric effect and the Compton effect both demonstrate the particle characteristics of a photon supporting the notion of wave-particle duality. A natural consequence of this is to ask if a particle, such as an electron, could behave like a wave. Louis de Broglie introduced this idea in 1923. He proposed, based on Compton’s findings, that matter-possessing momentum has a characteristic wavelength according to ![]() .
.
For an electron travelling near the speed of light, this equation becomes ![]() .
.
The first evidence of matter waves came several years later when physicists C.J. Davison and L.H. Germer accidentally discovered that a beam of electrons can create an interference pattern. Ultimately, this discovery contributed to the development of the modern electron microscope.
 Watch and Listen
Watch and Listen
Open “de Broglie Waves” to see a demonstration of de Broglie's work.
 Read
Read
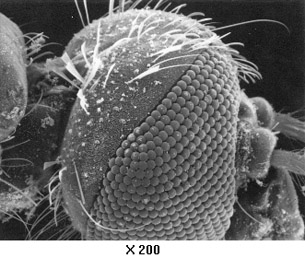
© Musem of Science, Boston
Read “Then, Now and Future, The Electron Microscope” on page 727 and “De Broglie’s Wave Hypothesis: Strange but True!” on page 729 of your physics textbook.
As you discovered in the reading about electron microscopes, the magnification of a microscope depends on the inverse of the wavelength that produces the image. The electron microscope is able to generate matter waves with wavelengths much smaller than that of visible light, leading to greater magnification as you can see in the picture of the fly’s eye to the right.
Example Problem 1. What is the wavelength of an electron with a speed of 5.50 × 106 m/s? How many times smaller is this wavelength compared to a 400-nm red light?
Hint: When asked to compare two quantities, answer by stating how many times larger or smaller one quantity is relative to the other.
Given
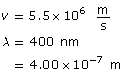
Required
the wavelength of the electron and the ratio of the wavelengths of the electron and red light
Analysis and Solution
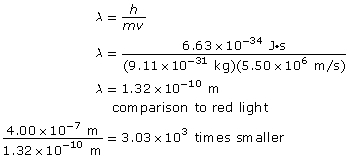
Paraphrase
The wavelength of the electron is 1.32 × 10–10 m, and it is 3.03 × 103 times smaller than the wavelength of red light.
Example Problem 2. What is the wavelength of an electron that has a kinetic energy of 3.10 × 10–16 J?
Given
![]()
Required
the wavelength of the electron
Analysis and Solution
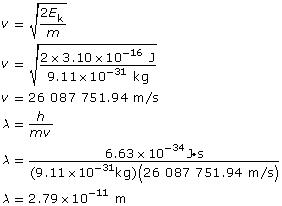
Paraphrase
The wavelength of the electron is 2.79 × 10–11 m.
 Self-Check
Self-Check
SC 3. What is the wavelength of an electron that has a speed of 2.25 × 107 m/s?
SC 4. What is the wavelength of an electron that has a kinetic energy of 7.5 × 10–4 MeV?
SC 5. What is the speed of an electron that has a wavelength of 7.00 pm?
SC 6. What is the wavelength of an electron that is accelerated from rest through a potential difference of 1000 V?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3.
Given
![]()
Required
the wavelength of the electron
Analysis and Solution
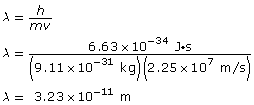
Paraphrase
The wavelength of the electron is 3.23 × 10–11 m.
SC 4.
Given
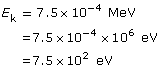
Required
the wavelength of the electron
Analysis and Solution
Change the energy in eV to J
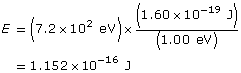
Use the kinetic energy to find the velocity.
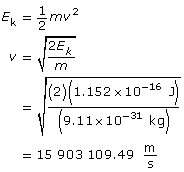
Use the velocity to find the wavelength.
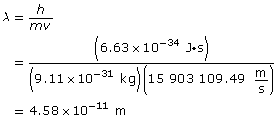
Paraphrase
The wavelength of the electron is 4.58 × 10–11 m.
SC 5.
Given
![]()
Required
the velocity of the electron
Analysis and Solution
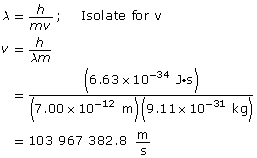
Paraphrase
The speed of the electron is 1.04 × 108 m/s.
SC 6
Given
V = 1000 V
Required
the wavelength of the electron
Analysis and Solution
Calculate the change in energy (or work done) of the electron.
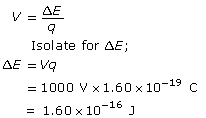
Calculate the velocity using ![]() .
.
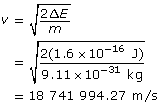
Calculate the wavelength.
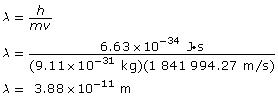
Paraphrase
The wavelength of the electron is 3.88 × 10–11 m.
 Read
Read
Heisenberg’s uncertainty principle: a principle stating that it is impossible to know both the position and momentum of a particle with unlimited precision at the same time
Read “De Broglie’s Hypothesis—A Key Concept of Quantum Physics” and “Heisenberg’s Uncertainty Principle” on pages 730 to 735 of the textbook.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remember to submit your answers to A 5, A 6, A 7, and A 8 to your teacher as part of your Module 6: Lesson 3 Assignment.
A 5. How did de Broglie’s wave equation show that energy and matter are similar?
A 6. A stationary hydrogen atom with a mass of 1.67×10-27 kg absorbs a photon of light with 10.2 eV. What is the velocity of the hydrogen atom after absorbing the photon in a perfectly inelastic collision?
A 7. If you performed Young’s experiment with high-speed electrons instead of light, what would the results look like? How does this support the wave or particle model?
A 8. What does Heisenberg’s uncertainty principle mean about physicists’ attempts to measure the size of the electron?
 Discuss
Discuss
De Broglie’s wave equation takes a simple mathematical form. His theory that a moving particle is associated with a wavelength, however, leads to some very interesting conclusions. For example, using the wave nature of particles and the concept of standing wave patterns, it is possible to explain why an electron can only have specific amounts of energy.
Based on these readings, answer the following:
D 1. Explain why a “particle in a box” can only have certain amounts of energy. Post your solution in the discussion area.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remember to submit your answer to D 2 to your teacher as part of your Module 6: Lesson 3 Assignment.
D 2. Read the solutions that two other students have posted. Use what you learn from their solutions to improve your own. Include comments on what you learned from the other two submissions.
Discussion Scoring Guide
Principles involved: Wave nature of matter, Heisenberg’s uncertainty principle |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. | Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. | Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. | Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. | The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. | The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. | The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable. |