Module 2 Summary
1. Module 2 Summary
Module 2 Summary
Using odds and probabilities can be useful in helping to make decisions in games and in many other aspects of life.

little league: Jupiterimages/Brand X Pictures/Thinkstock, poker winner: Fuse/Thinkstock,
chess players: Comstock/Thinkstock
In this module you
- interpreted and assessed the validity of odds and probability statements
- solved problems that involved the probability of mutually exclusive and non-mutually exclusive events
- solved problems that involved the probability of two dependent or independent events
You learned to determine the odds in favour of or odds against an event given the probability of that event, and you learned to determine the probability of an event given the odds for or against that event. You learned that those events with no common outcomes are known as mutually exclusive events and that those events without common outcomes are known as non-mutually exclusive events. You learned that when the outcome of one event has no effect on the outcome of another event, the events are known as independent events. If the outcome of an event affects the outcome of another event, the events are known as dependent events.
In Module 2 Project: Carnival Probabilities, you calculated and assessed the probabilities and odds of carnival games. You then used your understanding to design your own carnival game and assessed the odds and probabilities associated with the game.
Below are some of the key ideas that you learned in each lesson.
In Lesson 1 you learned that odds and probabilities are used in daily life and play an important role in making decisions.

Hemera/Thinkstock
Imagine that these doors are used on a game show on TV and behind two of the doors is a prize. The probability of winning a prize is ![]() the odds in favour of winning a prize are
the odds in favour of winning a prize are ![]() or 2 : 3, and the odds against winning a prize are 3 : 2.
or 2 : 3, and the odds against winning a prize are 3 : 2.
![]()
or
odds in favour of A = number of outcomes for A : number of outcomes against A
![]()
In Lesson 2 you learned that some events have no common outcomes and these are known as mutually exclusive events, whereas other events share common outcomes and these are known as non-mutually exclusive events.
This is the formula for mutually exclusive events.
P(A or B) = P(A) + P(B)
or
P(A ∪ B) = P(A) + P(B)
This is a diagram of mutually exclusive events.

© Mannaggia/23299310/Fotolia
This is the formula for non-mutually exclusive events.
P(A or B) = P(A) + P(B) − P(A and B)
or
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
This is a diagram of non-mutually exclusive events.
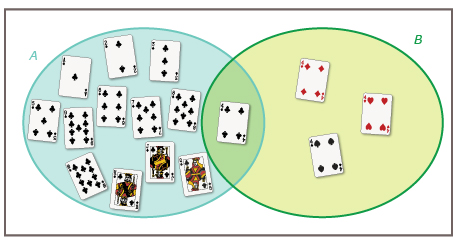
© Mannaggia/23299310/Fotolia
In Lesson 3 you learned that independent events are those where the outcome of one event does not affect the outcome of another and dependent events are those where the outcome of one event does affect the outcome of another.
This is the formula to use for independent events.
When two events, A and B, are independent, the probability of both occurring is
![]()
You used the gizmo titled Compound Independent and Dependent Events to discover more about independent events. The following picture shows independent events. The total number of marbles remains the same after each draw.
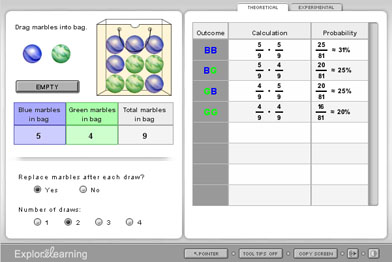
Screenshot reprinted with permission of ExploreLearning
This is the formula to use for dependent events.
When two events, A and B, are dependent, the probability of both occurring is
![]()
The following picture shows dependent events. The total number of marbles changes after each draw.
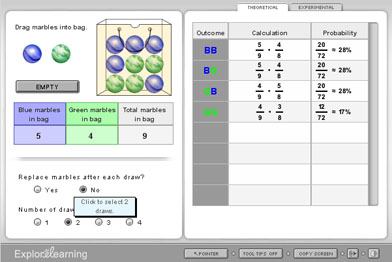
Screenshot reprinted with permission of ExploreLearning