Module 4
1. Module 4
Module 4 Introduction
This module involves the study of polynomial functions. Polynomial functions can be used to model real-world problems, such as the path of a projectile, the revenue that a drama production will produce, or even a recipe. Imagine that you are making pancakes in the morning and the recipe looks something like this:
1 cup flour
![]() cup sugar
cup sugar
![]() cup milk
cup milk
2 eggs
![]() teaspoon of vanilla
teaspoon of vanilla
Think of these ingredients as variables and the amounts as the coefficients. You can make an equation of the recipe that would look something like this:
![]()
If you wish to double the amount of pancakes, you would multiply everything by 2:
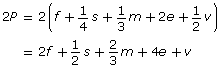

Adapted from IT Stock Free/Polka Dot/Thinkstock
Simple polynomial functions can also be graphed to determine maximum, minimum, symmetry, and domain and range. Polynomial functions can be seen in the shapes of many things in the environment around you. You will be exploring these functions throughout this module.
Polynomial functions are also used to approximate other more complicated functions.
In this module you will investigate the following question: How can polynomial functions be used to model problems?
To investigate the module question, you will focus on the lessons and questions in the following table.
| Lesson | Title | Lesson Questions |
| 1 | Polynomial Functions and Their Graphs | How are the characteristics of the graph of a polynomial function related to the degree of the polynomial? |
| How are the characteristics of the graph of a polynomial function related to the leading coefficient and constant term? | ||
| 2 | Modelling Data with Lines of Best Fit | How can a line of best fit be used to model problems? |
| 3 | Modelling Data with a Curve of Best Fit | How can a curve of best fit be used to model problems? |
The Module 4 Project: Graphic Design Using Polynomials will focus on exploring and analyzing shapes of polynomials in your environment.
Note: Loading times for video and other media may vary depending on your Internet connection. Please be patient.