Explore 3

Math 10C Module 1 Lesson 8

Module 1: Measurement and Its Applications

 

Try This 4

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson).
TT 4. Complete “Exercises” questions 6, 7, and 11 on pages 101 and 102.

Use the link below to check your answers to Try This 4.

Possible TT4 (Try This 4) Solutions

Self-Check

Choose the correct answer.

SC 1. In a triangle, the sum of all angles equals ________.

A. 180°
B. 90°
C. 360°
D. There is not enough information given to answer this question.

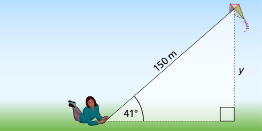
This graphic shows a kite on a 150-m long string at an angle of elevation of 41°.

SC 2. A kite has a string 150-m long. If the string makes an angle of 41° with the ground, find the height of the kite above the ground.

A. 98 m

B. 113 m

C. 150 m

D. 168 m

 

 

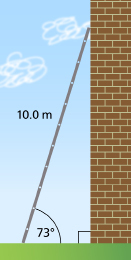
This graphic shows a 10.0-m ladder leaning against a wall. The ladder makes an angle of 73° with the ground.

SC 3. A 10.0-m ladder leans against a vertical wall. The angle between the ladder and the ground is 73°. Find the distance from the foot of the ladder to the wall.

A. 2.9 m

B. 7.6 m

C. 9.6 m

D. 15.9 m





This graphic shows an illustration of a hot-air balloon containing a person whose line of sight to an object on the ground creates an angle of depression with the horizontal.

woman © Volume 43 Everyday Woman/Getty Images

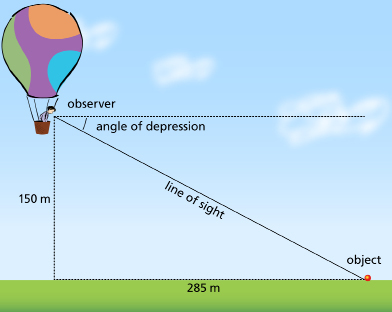
SC 4. A person in a hot air balloon is 150 m above the ground. An object is 285 m away from the balloon on a line directly beneath the balloon. What is the angle of depression of the person’s line of sight to the object on the ground rounded to the nearest degree?

A. 28°

B. 32°

C. 62°

D. 58°

Caution

 

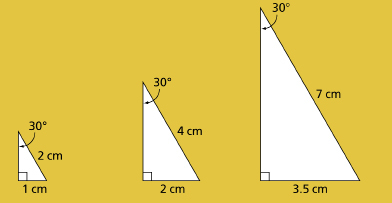
It is important to realize that the same angle can be produced from many different triangles. You should observe that, although the side lengths that make up the triangle may vary, the value of a ratio, such as sin 30°, does not vary.

 

This graphic shows three right triangles of different sizes, each with a 30° angle. The hypotenuse and base of each triangle, in order from left to right, are 2 cm and 1 cm; 4 cm and 2 cm; 7 cm and 3.5 cm.

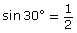
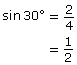
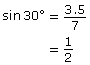
eqn093.eps          eqn094.eps           eqn095.eps

 



Compare your answers.

 

Some trigonometry problems need to be modelled with two triangles. For this type of problem, you will need to determine the measure of either a length or an angle from each triangle. You may need to calculate the measure of a length or angle on one triangle before you can determine the length on another triangle.

 

This graphic shows an illustration of two right triangles sharing a common length of AC.

Example

 

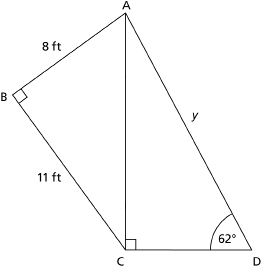
In the diagram, the given distances are as follows:

 

AB = 8 ft

BC = 11 ft

CD = 9 ft

 

What is the distance from point A to point D?

 

Solution

 The length AD is labelled y in triangle ACD. There is not enough information to solve triangle ACD. You would need to know the length of another side in triangle ACD in order to solve the triangle. However, there is enough information to solve triangle ABC.
Notice that triangles ACD and ABC have length AC in common. You can solve triangle ABC for length AC. Once you know the length of AC, you will have enough information to solve for all unknown measures of triangle ACD, including length AD.

 In triangle ABC,

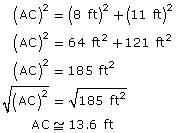
In triangle ACD, you now know the length of the side opposite 62°, and you are solving for the hypotenuse y.

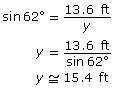
Read

 

Read the textbook that you are using for this course. Read through the following additional example to see how a trigonometry problem can be modelled by two right triangles. Pay attention to the extra step at the end. Why is this step necessary?

Foundations and Pre-calculus Mathematics 10 (Pearson)

 

Read “Example 2: Solving a Problem with Triangles in the Same Plane” on pages 115 and 116, which demonstrates how to solve a two-triangle trigonometry problem involving the height of a building.

 

Try This 5

 

Remember as you model and solve problems involving two triangles that you can only solve a triangle if you have enough information. If you don’t have enough information in one triangle, then you need to solve the other triangle to get the values you need for the first triangle.

 

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson).
TT 5. Complete “Exercises” questions 3.b), 9, and 11 on pages 118 and 119.

Use the link below to check your answers to Try This 4.

Possible TT5 (Try This 5) Solutions