Lesson 2: Square Roots and Cube Roots

Module 2: Roots and Powers

 

Read

Go to the textbook and work through the following examples to see how prime factorization is used to identify numbers as perfect squares or perfect cubes. This method also helps you to determine the square roots and cube roots of those numbers. As you read, focus on how the prime factors are regrouped into identical groups to find the square and cube roots.

 

Self-Check

 

SC 1. Use prime factorization to determine whether the number 3375 is a perfect square, a perfect cube, or neither. If it is a perfect number, state the square root or cube root.

You may wish to use the applet “Prime Factorization” you used in Lesson 1.

SC 2. Identify each of the following numbers as a perfect square, a perfect cube, both, or neither: 16, 125, 64, 32.

Compare your answers.

 

Guess and Check

Guess and check can be a very useful method in math, especially if you are re-examining your choice after each guess so you can get closer and closer to the answer.

You might be asked to find out if 1728 is a perfect cube. Here is one way you can use guess and check:

10 × 10 × 10 = 1000

You need 1728, which is greater than 1000, so you need a number greater than 10.

13 × 13 × 13 = 2197

You need 1728, which is less than 2197, so you need a number less than 13 and greater than 10.

12 × 12 × 12 = 1728

Therefore, 1728 is a perfect cube since its cube root is 12.

What if the number is not a perfect cube? What would your guess and check look like? If you were asked if 340 was a perfect cube, you would go though similar calculations:

10 × 10 × 10 = 1000

You need 340, which is less than 1000, so you need a number less than 10.

5 × 5 × 5 = 125

 You need 340, which is greater than 125, so you need a number greater than 5.

7 × 7 × 7 = 343

You need 340, which is less than 343, so you need a number less than 7.

6 × 6 × 6 = 216

You need 340, which is greater than 216, so you need a number greater than 6.

Uh-oh. So you find you need a number greater than 6 but less than 7. How is that possible? Well, it means your answer will be a decimal number between 6 and 7.

Therefore, 340 is not a perfect cube since its cube root is a decimal number.

 

Calculator Method

 

While you could continue with the guess-and-check method to find the cube root of 340, a faster way would be with a calculator.

 

Example 1

 

Evaluate 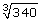with your calculator. Round your answer to 4 decimal places.

 

Solution

 

The keystrokes will vary depending on your calculator. Consult your calculator menu for the keystrokes appropriate for your calculator. Two possible sequences are provided here.

scientific calculator:

graphing calculator: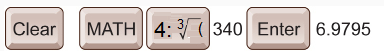

or

Read

There are multiple methods for finding square roots and cube roots. In fact, there are even variations of the same method! Go to the textbook and read the following examples. Can you find the differences in the ways these methods are presented in the lesson compared to the textbook examples?

 

You have learned how to identify and determine square roots and cube roots. Now you can begin to apply those strategies to solving problems. As you do so, recall the chart that helps you to organize and plan your approach to these problems.

 

Read the Problem	Explore	Select a Strategy	Solve	Look Back
Note key words. What is known? What is unknown? What are you asked to find? Restate the problem.	Organize the information. Picture the problem. Draw a diagram or table. Do you know a related problem that could help?	Here are just a few: pattern recognition working backwards guess and check reduce or simplify	Carry out your strategy.	Check your answer(s). Does it make sense?

 

Example 2

A cube can hold 729 cm3 of sand. Show how you could use two different strategies to calculate the length of its side.

Solution

Since it is a cube, you know all sides (length, width, and height) are the same. So, you need a number that can multiply by itself three times to get 729.

729 = side × side × side

Strategy 1: Guess and Check

6 × 6 × 6 = 216	So you know you need a number more than 6.
10 × 10 × 10 = 1000	So you know you need a number less than 10.
9 × 9 × 9 = 729	So you have it!

 

Strategy 2: Prime Factorizaton

You can also use the prime factorization method to find the cube root of 729.

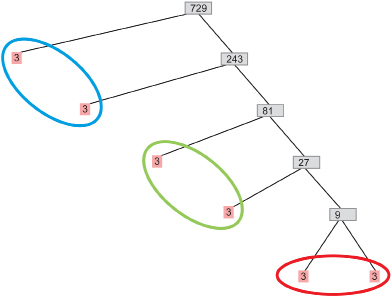
There are three groups of 3 × 3, so you can write 729 as 93.

Strategy 3: Using a Calculator

If you are not a fan of trial and error, you could also find the cube root of 729.

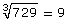
 So this means 9 × 9 × 9 = 729.

 

Self-Check

 

SC 3. Adam wants to make some extra money over the summer, so he decides to mow lawns. His neighbour has a square lawn with an area of 576 ft2.

2. What are the dimensions of his neighbour’s square lawn?
3. As Adam collects the grass clippings, he adds them to his plastic cube bin. The bin has a volume of 7415 in3. What are the dimensions of the cube bin to the nearest tenth of an inch?

SC 4. Can a negative number be a perfect square? Can it be a perfect cube? Explain your answers.

 

Compare your answers.

 

Try This 5

Practise applying the concepts of square roots and cube roots to these problems in your textbook. Read the questions carefully as they may require you to do more than one step.

 

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 5. Complete “Exercises” questions 4.b), 5.c), 6.b,  6.d), 9, 11and 14 on pages 146 and 147.

Use the link below to check your answers to Try This 5.

Possible TT5 (Try This 5) Solutions

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education