Lesson 2: Square Roots and Cube Roots
Module 2: Roots and Powers
Lesson 2: Square Roots and Cube Roots
Focus
In the last lesson you discovered how the mathematics of prime numbers are used in the encryption and decryption of codes. One of the best-selling toys since the 1980s is a puzzle that can be easily encrypted, but not so easily decrypted.
The Rubik’s Cube, invented in 1974 by Hungarian sculptor Emo Rubik, is a three-dimensional mechanical puzzle. The classic Rubik’s Cube has six faces, with each face composed of nine smaller panels. These panels are covered with red, orange, yellow, green, white, or blue stickers. The cube is designed so that each face can be pivoted. To encrypt the cube, you must pivot the faces to mix the colours. To decrypt the cube, or to solve the puzzle, the cube must be pivoted until each face is a solid colour again.
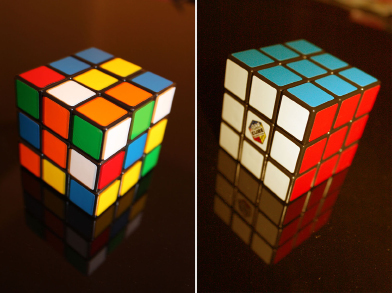
By looking at the photos of the Rubik’s Cube, you can see that each face is composed of 9 smaller cubes. Since it is possible to make a square face out of 9 cubes by placing them in a 3 × 3 arrangement, 9 is considered a perfect square. The square root of 9 is 3 because 3 represents the side length of the square.
You can also see that the entire Rubik’s Cube is composed of 27 smaller cubes. Since it is possible to make a cube out of 27 cubes by placing them in a 3 × 3 × 3 arrangement, 27 is considered a perfect cube. The cube root of 27 is 3 because the cube root represents the side length of the cube.
In this lesson you will learn how to determine whether other numbers are perfect squares or perfect cubes. You will also learn how to calculate square roots and cube roots.
Outcomes
At the end of this lesson, you will be able to
- determine, concretely, whether a given whole number is a perfect square, a perfect cube, or neither
- determine, using a variety of strategies, the square root of a perfect square and explain the process
- determine, using a variety of strategies, the cube root of a perfect cube and explain the process
- solve problems that involve square roots or cube roots
Lesson Questions
- How can you choose the best strategy for determining square roots and cube roots?
- How are square roots and cube roots used to solve real-world problems?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**