Math 10C Module 2 Lesson 2

Module 2: Roots and Powers

 

Lesson Assessment

This shows a computer-created illustration of cube-shaped gift-wrapped boxes.

© Chris Harvey/shutterstock


Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete. 

Project Connection **NOT ASSIGNED **

 

A cipher is a procedure for encrypting or decrypting secret messages. One way to encode a message is by using a substitution cipher where each letter in the message is substituted by a number.

Retrieve your grid of the prime numbers less than 100 from Lesson 1. Notice that there are 25 primes less than 100. Since there are 26 letters in the alphabet, you can choose a letter to be unassigned (for example, you could leave Q unassigned and use K when your code calls for a Q) or you could make use of the next prime number (greater than 100), which is 101.

 

Using this last method, your table of substitutions looks like this:

 

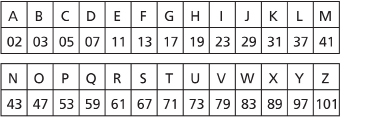
m10c_m2_019.jpg

 

You can use this method to encode the expression “I LOVE MATH.”

 

Step 1: Use the table to determine the corresponding prime number substitutions for each letter in the code.

 

23 37 47 79 11 41 02 71 19

Step 2: Write the numbers together.

 

233747791141027119

(By writing the numbers together, you can hide the fact that each number represents a letter.)

You can also use this method to decrypt the code: 410271192367137343.

Step 1: Break the code into pairs of digits.

 

41 02 71 19 23 67 13 73 43

Step 2: Use the table to determine the corresponding letter substitutions for each prime.

 

M A T H I S F U N

Step 3: Use reasoning to determine where the words begin and end.

 

MATH IS FUN

The problem with substitution ciphers is that they are easy to figure out. A person could use letter frequencies to break the code. In the first two lessons of this module, you used prime factorization to determine GCF, LCM, square roots, and cube roots. How can you use prime factorization as a cipher?

Encode the expression “I LOVE MATH.”

Step 1: Break the phrase into three-letter blocks.

 

ILO VEM ATH

 Step 2: For each block of letters, multiply the prime number substitutions together.

 

ILO = 23 × 37 × 47 = 39997

 

VEM = 79 × 11 × 41 = 35629

 

ATH = 2698

This is the first part of your code.

Step 3: Think: If the three letters in each block were to be arranged in alphabetical order, which one would be first, second, and last? Assign each letter a number from 1 to 3 depending on the position of the letter in an alphabetical arrangement of the letters.

 

ILO = 123

 

VEM = 312

 

ATH = 132

This is the second part of your code.

Step 4: Put the first and second parts of the code together.

 

39997-123

 

35629-312

 

2698-132

 
 
 
 
 
 
 
 
 

5822-213

You can decrypt the code 29279-123 by following this procedure:

 
 
 
 
 
 
 
 
 

40807-132

 Step 1: Perform the prime factorization of the first part of each number. Since the numbers are large, you may want to use the prime factorization applet used in this lesson to simplify the calculations. Write the factors initially in order from least to greatest.

 

5822 = 2 × 41 × 71

 

29279 = 19 × 23 × 67

 

40807 = 13 × 43 × 73

Step 2: Rearrange the factors of each number in the order described by the second part of each number.

Since the sequence for 5822 is 213, this means the correct arrangement of factors in the prime factorization is the second factor, then the first factor, and then the third factor.

 

5822 = 41 × 2 × 71

Similarly, for 29279, since the second part is 123, this means to write the first factor first, the second factor second, and the third factor last.

 

29279 = 19 × 23 × 67

 

40807 = 13 × 73 × 43

Step 3: Write all the factors together.

 

41 2 71 19 23 67 13 73 43

Step 4: Use the grid to convert the primes into letters.

 

M A T H I S F U N

 

The message is “MATH IS FUN.”

Reflect on these questions:

  1. Why were the letters put into three-letter groups before encoding? What would happen if the message was not broken into smaller groups of letters?
  2. Why is it necessary in this method to add an extra three digits at the end of the number?
  3. How is the cipher based on prime factorization more difficult to break than the substitution cipher originally introduced?

At this time, go to the Unit 2 Project and complete the Module 2: Lesson 2 portion of the project.

 

Going Beyond

 

In this lesson you used the method of prime factorization to determine the square roots and cube roots of natural numbers. Fortunately, those natural numbers were small enough that they could be factored in a relatively short amount of time.

 

There are certain tests that you can perform to quickly know whether a natural number, n, is divisible by other numbers. For example, you may know that n is divisible by 2 if n is even. You may also know that n is divisible by 10 if the last digit is 0.

 

Use reasoning and search the Internet to discover what the tests of divisibility are for the numbers from 2 to 10. You may want to use the search terms “tests of divisibility.”

 

Divisor

Test

2

If the last digit is even, then the number is divisible by 2.

3

  

4

  

5

  

6

  

7

  

8

  

9

  

10

  

 

Use your reasoning ability to determine what tests of divisibility may exist for other numbers. How can knowing whether a number, n, is divisible by a greater number help you in prime factorization?