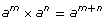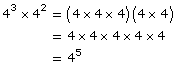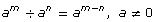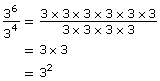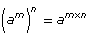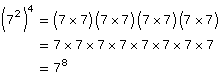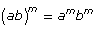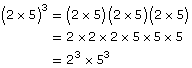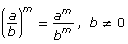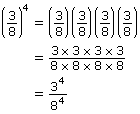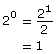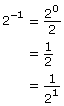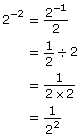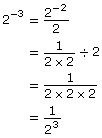Math 10C Module 2 Lesson 5

Module 2: Roots and Powers

 

Explore

This shows a photo of a young man with spiky hair.

© Gina Smith/shutterstock

 

Exponents can be used to describe very large numbers and very small numbers. For example, the number of strands of hair on a person’s head is about 1.0 × 105, while the diameter of a single strand of hair can be as small as 2.0 × 10−5 m. If you laid each strand of hair side by side, what would be the distance from one end to the other? In this lesson you will review the exponent laws and learn other ones that will help you solve questions like this.

 

Glossary Terms

 

Add the following terms to your "Glossary terms":

  • base
  • exponent
  • power
  • reciprocal

----------------------------------------------------------------

In your previous math courses, you studied the exponent laws. The following chart summarizes those exponent laws. The chart also provides examples for you to see why each law works. Read over this chart carefully. There is chart to print, later in this section.

Exponent Law

General Case

Example

Product Law

Quotient Law

Power of a Power

Power of a Product

Power of a Quotient

 

Zero Exponents

It is easy to think of the expression 23 as three factors of 2 multiplied together. In other words,

 

23 = 2 × 2 × 2

While this is true for all values of the exponent that is a natural number, in the case of 20, it is not appropriate to think of the power as zero factors of 2 multiplied together. In fact, if you thought of it this way, you might think the answer is zero. After all, the absence of any factors should leave you with nothing! However, if you look at your chart from the licorice investigation in the Discover section, you will see that this is not true.

In that investigation you used patterns to complete the table. Starting with 8, each number in the first row is half of the previous number. That is because you were always removing (or eating) half of the amount of licorice that was left. In the second row, you expressed each number in the first row as a power of 2, starting with 23, then 22, then 21, and so on with the exponent diminishing by one each time.

According to the pattern, what was the value equal to 20?

You can verify this result algebraically using the laws of exponents.

You know the quotient law states that

Then it follows that

 

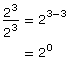
This rule applies to bases other than 2. Suppose the base is assigned the variable a:

 

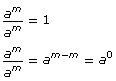
Therefore, 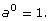This is the zero exponent law. This law can be added to the chart above.

Negative Exponents

Just as it is difficult to think about zero factors of 2 multiplied together in the case of the expression 20, it is perhaps even more difficult to think about negative three factors of 2 multiplied together. That just doesn’t make sense!

Refer again to your chart from the licorice investigation. Consider the expanded form of each power of 2:

 

23 = 2 × 2 × 2

 

22 = 2 × 2

 

21 = 2

 Do you see that each time you decrease the exponent by 1, you are dividing by a factor of 2? What will happen if you continue this progression?

 

A negative exponent means to divide by that number of factors instead of multiplying! So 5−3 is the same as This pattern reveals the general rule that where (You can also rearrange the equation to get where )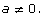

This is called the integral exponent law. This law can be added to the chart above.

Exponents Law Chart

Please print and store in your course folder ( binder) for future reference.

Exponent Laws

20 = 1

Â