Lesson 3: Common Factors and Factoring Trinomials
Module 3: Polynomials
Explore

© bhowe/shutterstock
To factor a polynomial means to express it as a product. In the same way that a refrigerator cools food and a microwave oven warms food up again, multiplying polynomials and factoring are inverse operations. In other words, what can be done with one operation can be “undone” with the other operation. This concept is helpful when you are checking a solution. You can check the result of factoring by multiplying the factors. If the product is the same as the original polynomial, then you have factored correctly.
Just as there are multiple strategies for multiplying polynomials, there are also multiple strategies for factoring them. In this lesson you will investigate two strategies. The first one is applicable to all polynomials, and the second is a more specific one that applies to trinomials of the form x2 + bx + c.
Glossary Terms
Add these terms to your "Glossary Terms" in your notes:
- common factor
- factor
----------------------------------------------------------------
When you are required to factor a polynomial, the first task is to see if you can find a greatest common factor, or GCF. This is the first strategy you will investigate in this lesson.
In the Math Lab, you arranged tiles into rectangular areas. Did you notice that area of the rectangle is equal to the product of the dimensions? For example, to factor 2x + 4, you could take two x-tiles and four 1-tiles and arrange them as follows.
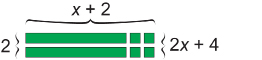
The dimensions of this rectangle are 2 by x + 2. As a result, you can express 2x + 4 as a product of its factors:
2x + 4 = 2(x + 2)
When you look at the factors, they cannot be broken down any further. In other words, x and 2 have no other common factors. Therefore, the binomial 2x + 4 has been completely factored.
 Caution
Caution
You may have also found that you can arrange the 2x + 4 tiles as a rectangle with dimensions 1 by 2x + 4.
![]()
While this is fulfilling the requirement of creating a rectangle from the available tiles, it is does not completely factor the polynomial. After all, 1(2x + 4) is still 2x + 4.
 Watch and Listen
Watch and Listen
Watch the video “Using the Area Model to Illustrate Common Factoring”.
An alternate way to factor a polynomial is to divide each term by the GCF.
Example
Factor the binomial 5x3 – 75x.
Step 1: Express each term in the polynomial as a product of its prime and variable factors.
![]()
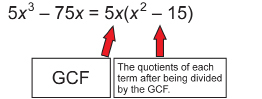
Step 2: Identify the factors that both terms have in common; then multiply them together. Each term has a factor of 5 and x.
![]()
Step 3: Divide each term by the GCF and report the answer.
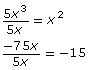
Therefore,
Step 4: Check your answer by using the distributive property to expand the expression.
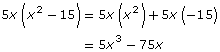
 Read
Read
Go to your textbook to reinforce the examples that have been shown. As you study the examples, try to find out when it would not be possible to factor a polynomial by arranging algebra tiles in the shape of a rectangle.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read pages 152 to 154. This includes the following:
- “Example 1: Using Algebra Tiles to Factor Binomials”
- “Example 2: Factoring Trinomials”
Next, read “Example 3: Factoring Polynomials in More than One Variable” on page 154.
 Tip
Tip
Whenever you need to factor a polynomial, the first thing you should do is to check whether the terms of the polynomial share a common factor. If so, you can use the GCF method to factor the polynomial. By doing so, you will be able to work with smaller numbers.
 Self-Check
Self-Check
SC 1. For each of the following polynomials, factor and state the GCF.
- 12x – 16
- 12x2y + 6xy2
- 4x3 + 2x2 – 6x
- –4x2y + 2xy
 Tip
Tip
When factoring by common factors, be sure that you factor the GCF out of all of the terms.
 Try This 1
Try This 1
Complete the following in your course folder ( binder). Show all work.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” questions 4.a), 4.b), 8.a), 8.c), 10.b), 10.d), 10.f), 16.b), 16.d), 16.f), and 17 on pages 155 and 156.
Use the link below to check your answers to Try This 1.
