Lesson 3: Common Factors and Factoring Trinomials

                                        Module 3 Polynomials                                         

Part 2: Factoring Trinomials

There are many methods of factoring trinomials. How you decide which method to use will depend on the properties of the trinomial. In the remainder of this lesson you will focus on the methods used to factor trinomials of the form x² + bx + c, where b and c are integers. NOTE: there is no number written in front of the squared term which indicates there is a 1 there.

Area Method

As you learned in the Math Lab, one way to factor trinomials is by using algebra tiles to form a rectangular area.

Watch and Listen

Watch the video “Mathcast 010 Using the Area Model to Factor Trinomials” into a search engine. This videod shows you some more examples of how trinomials can be factored this way. Watch Example 1, it finishes at 3:31. (There are more examples done here  -  we will revisit this video in Lesson 4 to look at these). 

Self-Check

SC 2. Now that you have seen examples of how to use the area method to model the factoring of a trinomial, try the following Self-Check questions. Use algebra tiles or “Arranging Algebra Tiles” to factor each trinomial.

1. x² + 8x + 15
2. x² – x – 2

Compare your answers.

Product-Sum Method

Retrieve the Math Lab work from your course folder and review it. Examine your responses for “Analysis” questions 4.b. and 4.c. Did you notice a relationship between the numbers in the trinomial and the constants in the binomial dimensions?

Try the next activity to confirm your observations.

Try This 2 - 4

Complete the following in your course folder ( binder).

TT 2. Complete the first four rows of the table.

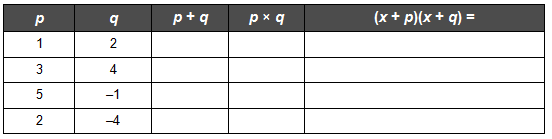
TT 3. Compare the numbers in the third column with the coefficients of the x-terms in the final column. What do you notice?

TT 4. Compare the numbers in the fourth column with the constants in the final column. What do you notice?

Use the link below to check your answers to Try This 2 - 4.

Possible TT2-4 (Try This 2-4) Solutions

The same result can be shown by a general expansion, where p and q represent any integer.

 

This expansion shows that the middle coefficient of the product of (x + p)(x + q) will always be the sum p + q, and the constant will be p × q.
           ------------------------------------------------------------------------------------------------------------------------------------------
This result leads to the product-sum method for factoring trinomials.
Do the following to factor a trinomial of the form x² + bx + c using the product-sum method:

Step 1: Find two numbers whose product equals c and whose sum equals b.

Step 2: Write these numbers as the constant terms in two binomial factors, where each binomial has x as its first term.
          ---------------------------------------------------------------------------------------------------------------------------------------------------

Example 1  Factor x² + 8x + 15.

Solution  The first step is to find two numbers whose product equals c and whose sum equals b. Use a table to determine the integers whose product equals 15.

p	q	Product	Sum
1	15	15	16
3	5	15	8

Choose the combination that gives the correct sum. (In this example, the correct sum is shown in the second row of the chart.)
The next step is to express the polynomial as a product of its factors.
x² + 8x + 15 = (x + 3)(x + 5)

Read

Go to your textbook to study further examples of factoring trinomials of the form x² + bx + c. Pay careful attention to how factoring is accomplished when one or more terms in the trinomial is negative. What additional considerations are necessary when dealing with a negative product or a negative sum? 

Foundations and Pre-calculus Mathematics 10 (Pearson)  Read “Example 2: Factoring Trinomials” on page 163 and “Example 3: Factoring a Trinomial Written in Ascending Order” on page 164.

Watch and Listen

Watch this short recording that gives some help on how to be sure you have the entire set of factors when factoring a trinomial.

In some instances, you may have to apply more than one factoring technique before the trinomial is completely factored. Study the following example to learn how to approach this type of problem.

Example 2 Factor –3m² – 12m + 36.

Verify by doing the following:

• multiplying the factors
• substituting m = 1

Solution Complete the following steps.

Step 1: Factor out the greatest common factor, where possible. Each term is divisible by –3.

–3m² – 12m + 36 = –3(m² + 4m – 12)

Step 2: Find two numbers, p and q, such that

• p × q = –12
• p + q = 4

Use a table to determine the integers whose product equals –12.

p	q	Product	Sum
1	–12	–12	–11
2	–6	–12	–4
3	–4	–12	–1
4	–3	–12	1
6	–2	–12	4
12	–1	–12	11

 Choose the combination that gives the correct sum of 4. In this case, you will use the values in the fifth row.

Step 3: Express the polynomial as a product of its factors.
-3m² - 12m+ 36 = -3( m² + 4m - 12)

                        = -3 ( m + 6) ( m - 2)

Now you can verify. First, you can multiply the three factors in any order.

Since this result is the same as the original trinomial, the factors are correct.

Then, substitute m = 1 into the trinomial expression as well as the factor expression.

–3m2 – 12m + 36	3(m + 6)(m–2)
Left Side = Right Side

There are trinomials of the form x² + bx + c that cannot be factored over the integers. In the case of
x² + x – 1, for example, there is no pair of integers whose sum is 1 and whose product is –1.

----------------------------------------------------------------------------------

 Tip

Try This 5

Practice applying the methods of factoring trinomials. Complete the following in your course folder ( binder), showing all work

Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 5. Complete “Exercises” questions 4, 14.a), 14.c), 14.e), 14.g), 15.d), 21.b), 21.d), and 21.f) on pages 166 and 167.

Use the link below to check your answers to Try This 5.

Possible TT5 (Try This 5) Solutions

Self-Check

As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur in their application. Some of these errors are due to inattention to details but do not imply student misunderstanding. Other types of errors reveal a misconception of the recently learned math principles.
The following examples show how a student may factor a polynomial using the methods learned in this lesson. In each case, the student has made an error. Your job is to identify and to correct the error.

SC 3. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.

1. Factor 10x³ + 15x² + 5x.
   10x³ + 15x² + 5x = 5x(2x² + 3x)
2. Factor x² – 5x – 6.
   Find two numbers whose product is –6 and whose sum is –5. The numbers are –3 and –2. Therefore, the factors are (x – 3)(x – 2).
3. Factor 2x² + 2x – 24.
   Find two numbers whose product is –24 and whose sum is 2. The numbers are 6 and –4. Therefore, the binomial factors are (x – 4)(x + 6).

Compare your answers.

  Try This 6

Identify the error and correct the solution. How can a student know if there is an error in his or her solution?
Complete the following in your course folder ( binder), showing all work

Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6.  a.   Complete “Exercises” question 12 on page 155.
        b.   Compete “Review” question 14 on page 199.

Use the link below to check your answers to Try This 6.

Possible TT6 (Try This 6) Solutions