Math 10C Module 5: Lesson 5

Module 5: Linear Functions

Self-Check

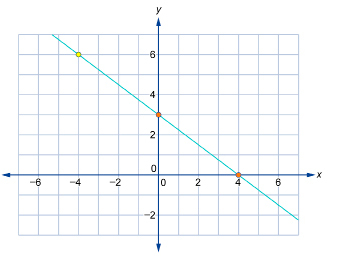
SC 3. Consider the linear function 3x + 4y − 12 = 0. Sketch the graph of this function. Describe the steps you followed. Check your answer by using graphing technology. (You may have to rearrange the graph so that the variable y is isolated before you can enter the expression into your calculator.)

Compare your answers.

Share 1 - 4

The two-intercept method allows you to find two points on a line—the minimum required to sketch a line. It is possible, and sometimes more convenient, to find two other points on a line besides the intercepts.

Work with a partner  ( if possible) to answer the following questions. Complete these in your binder.

  1.   Describe how you can find two integral points (points with integer coordinates) on the line represented by the equation 5x + 3y - 8 = 0. Then sketch the graph.

  2.   When constructing a line, why is it better to use points that have integer coordinates?           

  3.   How can you use technology to locate integral points?

  4.   If you can only find one point, how can you still graph the line?

Possible S1 - 4 Solutions

 

Verifying a Graph

It is a very good habit to check to make sure your graph is correct, especially when you are solving for the x- and y-intercepts. There is a lot of algebra in this process, and one little mistake can lead you to an incorrect graph.

One way you can verify a graph is by checking that two points on the graph satisfy the equation of the line. Every point on the graph of a linear function will satisfy the equation of that linear function. This means that when you substitute the coordinates of any point on a line into the equation of that line, you will obtain a true statement. When verifying, you should choose at least one point on the graph that was not one of the original points used to graph the line.

Example

Verify the graph used in SC 3.

Solution

Look for another point on the graph; then substitute the coordinates of that point into the original equation. The point (−4, 6) appears to be on the graph.

 

This shows a graph of a line passing through the points (0, 3), (4, 0), and (−4, 6).

Verify the point (−4, 6). Substitute x = −4 and y = 6 into the equation 3x + 4y − 12 = 0.

 

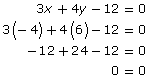
Since the left side is equal to the right side, the point satisfies the equation. Therefore, the graph is probably correct. Now verify a second point.

Verify the point (4, 0). Substitute x = 4 and y = 0 into the equation 3x + 4y − 12 = 0.

 

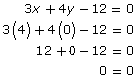
Since the statement 0 = 0 is true, the point satisfies the equation. Therefore, the graph is correct.

Other ways to verify a graph include:

->using graphing technology. Enter the equation into a graphing calculator or use graphing software; then check that the graph matches the one that has been manually constructed.

 -> verifying by rearranging the equation into slope-intercept form to see if the slope and y-intercept match the one that has been manually constructed.

 ->verifying by finding coordinates (x, y) that satisfy the equation. Then check to see if that point is on the graph. ( see above)
Here is the help document again for graphing a line using your  graphing calculator.
Graphing using a Graphing Calculator

 If you have graphed a line using your calculator ( graph y = 2x + 1) and you would like to look at a table of values, go 2nd graph to access the table feature.

Using a point on the graph to find b.
Given the point ( -2, 3) is on the line described by y = -4x + b, find b.
Solution:
Sub the point into x and y in the equation and solve for b. Replace x with -2 and y with 3.
y = -4x + b
3 = -4(-2) + b
3 = 8 + b
3 - 8 = b
b = -5

Self-Check

SC 4. For each equation, do the following:

  • Create an accurate sketch. Show all work.

  • Verify that your sketch is accurate.

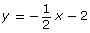
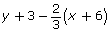
  3. x + 2y − 6 = 0

SC 5. Match each equation on the left with the corresponding graph on the right.

 

 

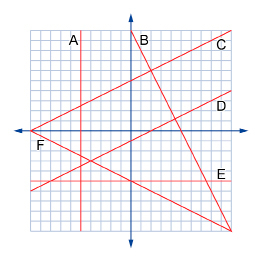
This shows a graph of six lines.

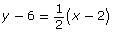
  2. x + 5 = 0
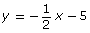
  4. 2x + y − 10 = 0
  5. y = −5
  6. x − 2y − 2 = 0

Compare your answers.

 

Try This 1 - 3

 

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)                         

TT 1. Complete “Exercises” questions 7.b), 7.d), 7.e), and 18 on pages 362 to 364.

TT 2. Complete “Exercises” questions 7.b), 7.d), 15.a), and 15.d) on pages 372 and 373.

TT 3. Complete “Exercises” questions 14.b), 14.d), and 22 on pages 384 and 385.

Use the link below to check your answers to Try This 1 - 2.

Possible TT1-3 (Try This 1-3) Solutions.