Lesson 6: Solving Problems with Linear Systems
Module 7: Systems of Linear Equations
Explore

iStockphoto/Thinkstock
The Tower of Hanoi puzzle.
To solve the Tower of Hanoi puzzle, you must move all the disks from one peg to another according to certain rules. You may only move one disk at a time. Also, the move may only be made to an empty peg or on top of a larger disc on a non-empty peg. Applying a certain sequence of steps allows you to solve the puzzle in a minimum number of steps.
(You may want to use your Internet search engine with the keywords “Tower of Hanoi” to learn more about this puzzle and to play an online version.)
In some ways, solving systems of equations is similar to solving the Tower of Hanoi puzzle. You have learned three methods of solving linear systems. Each of these methods requires that a certain sequence of steps be applied. The more you practise using these steps, the better you will become at solving linear systems!
 Read
Read
Consider different strategies for solving a problem that can be modelled by a system of linear equations. Go to your textbook and work through an example that shows how you can solve a problem with either graphing technology or by algebraic methods. As you read, consider the advantages and disadvantages of each approach. Also, consider other strategies that might work. Why do they work here? Which method do you prefer?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Using a Linear System to Solve a Problem” on pages 420 and 421.
In Lesson 2 of this module, you modelled various situations with systems of linear equations. In this lesson you will revisit those problems and solve them using both the algebraic and graphical methods that you have learned.
 Try This 1 - 4
Try This 1 - 4
At the beginning of Lesson 2, you created a system of equations to model the following problem:
Andrea has a bag of coins. There are 32 coins altogether, consisting of quarters and dimes. The total value of the coins is $5.90. Determine the number of quarters and the number of dimes in the bag.
Complete the following in your binder.
TT 1. Define the variables in the problem. Recreate the linear system that models this problem. Go back to your previous work to check that you have the correct set-up.
TT 2. Analyze your system and choose an appropriate strategy—graphing or algebraic—for solving the system. Then solve the system.
TT 3. Verify your solution quantitatively and qualitatively by doing the following steps.
a. Check that the solution values comply with the conditions stated in the problem.
b. Substitute the solution values in the original equations of the linear system.
TT 4. Once you have solved the system, evaluate your method. Was it the most appropriate strategy? Provide reasons to support your answer.
Use the link below to check your answers to Try This 1 - 4.
Possible TT1-4 Solutions
---------------------------------
The following example features a problem that you previously encountered in Lesson 2.
Example
Jennifer takes 5.9 h to drive her car 600 km from Edmonton to Dawson Creek. For the first part of the trip, her speed was 75 km/h, and for the rest of the trip her speed was 110 km/h.
- How long did she drive at each speed?
- How far did she drive at each speed?
Go to your course folder and retrieve your work related to this problem in Lesson 2 and do the following:
- Study how the linear system is established. Compare that with your own approach. Be sure that your approach leads to the same linear system.
- Solve the system using what you feel is the best method.
Then study the solution.
Solution
- Define the Variables
Let x = the time required to drive the first part of the trip.
Let y = the time required to drive the second part of the trip.
Organize the Information
Write the EquationsSpeed
Time
Distance
First Part of Trip
75
x
Second Part of Trip
110
y
The formula relating speed, time, and distance is d = st.
The equations of the linear system areSpeed
Time
Distance
First Part of Trip
75
x
75x
Second Part of Trip
110
y
110y
Total
x + y
75x + 110y
• total driving time: x + y = 5.9
• total distance driven: 75x + 110y = 600
Solve the Linear System
You can use substitution to solve this problem.
Rearrange the first equation.
y = 5.9 – x
Substitute the expression for y into the second equation.
75x + 110 (5.9 – x) = 600
Expand and solve for x.
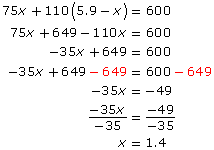
Substitute x = 1.4 into the equation y = 5.9 – x
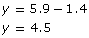
Jennifer drove for 1.4 h at 75 km/h; then she drove for 4.5 h at 110 km/h.
Verify the Solution
Check that the solution satisfies both equations in the linear system.
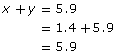
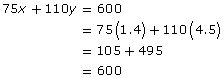
This solution also conforms to the conditions of the problem. The total time is 1.4 + 4.5 = 5.9 h. The total distance driven is 600 km. - Once you know the values of x and y, you can also determine how far Jennifer drove at each speed.
Refer to the chart used to organize the information. Use the expressions for distance to determine the length of each part of the trip.
First part of the trip:
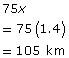 Second part of trip:
Second part of trip:
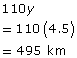
How is the solution strategy different from what you used to solve the problem?
 Share 6
Share 6
Complete the following.
Share 6 Questions.
Use the link below to check your answers to Share 6.
Possible S6 Solutions
----------------------------------
 Watch and Listen
Watch and Listen
Go to the site Writing Systems for some advice on how to set up the equations from word problems and to see a solved example.
----------------------------------
 Self-Check
Self-Check
For each of the following questions, do the following:
- Write a system of linear equations to model the situation.
- Choose a strategy and use it to solve the problem.
- Verify your solution; then evaluate the strategy that was used.
The key is figuring out whether to use the graph, substitution, or elimination strategy and deciding why one strategy may be better than the others.
SC 1. Two numbers have a sum of 60. Their difference is 6. Determine the two numbers.
SC 2. The mass of two bags of fertilizer differed by 10 kg. The larger bag contained 30% nitrogen. The smaller bag contained 20% nitrogen. The total mass of nitrogen in both bags was 16 kg. What was the mass of each bag?
 Try This 5
Try This 5
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 5. a. Complete “Review” question 13 on page 453.
b. Complete “Practice Test” questions 5.a) and 6 on page 455.
c. Complete “Cumulative Review” question 28 on page 461.
Use the link below to check your answers to Try This 5.
Possible TT5 Solutions
