Module 4

Module 4: Area

 

Bringing Ideas Together

 

Often estimating an area will help you decide whether or not a calculated answer is reasonable.

 

Example 1

 

A room measures 3.05 m by 3.96 m.

1. Estimate the room’s area.
   
   
2. Calculate the room’s area in square metres. Round to two decimal places.

Solution

1. Round each measure to the nearest metre.
   
   
   
   
   
   
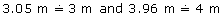
   So, the area of the room is about 3 m × 4 m = 12 m2.
   
   
2. 
   
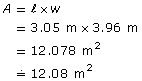
   This answer is reasonable, since the estimate was 12 m2.

Example 2

 

The top of a rectangular couch cushion is 23 in by 26 in. Jo wants to purchase enough material to cover the cushion.

1. Estimate the area in square feet.

2. Calculate the area in square feet. Round to two decimal places.

Solution

 

Watch the following animated solutions:

• “Example 2.a Solution”
• “Example 2.b Solution (Method 1)”
• “Example 2.b Solution (Method 2)”

Example 3

 

Estimate the number of square yards of carpet needed for a room that measures 14.5 ft × 12 ft.

 

Solution

 

Remember 1 yd = 3 ft. So, 14.5 ft is almost 5 yd, and 12 ft = 4 yd.

 

Therefore, the area is about 5 yd × 4 yd = 20 yd2. About 20 yd2 are needed to carpet the room.

 

In your work in Unit 1, you learned that, in Canada, many items are advertised in both imperial and SI units.

 

The following is a partial guide for your reference.

 

Square Foot	Square Yard	Square Metre
laminate flooring house and floor area lawn area on bags of fertilizer	carpets linoleum	laminate flooring carpets house and floor area linoleum lawn area on bags of fertilizer

 

Try This

 

TT 4. Try to add to the partial guide. Use the Internet or investigate a local building supply or home decorating store to expand the guide.

 

Save your work to your course folder.

 

Now, put your area estimation skills to work!

 

Self-Check

 

Answer the following questions. When you are finished, check your answers.

 

SC 2. Lunay’s rectangular driveway is 12.5 ft wide and 59 ft long.

1. Estimate the area in square yards.
   
   
2. Calculate the area to the nearest tenth of a square yard.
   
   
3. Compare your answer for question b to the estimate. What does the estimate tell you?

SC 3. A binder cover is 27 cm by 29 cm.

1. Estimate its area.
   
   
2. Calculate the area. Is your answer reasonable?

Compare your answers.

 

Estimating Areas of Shapes That Are Not Rectangular

 

In your work to this point, you have been calculating the areas of rectangles and squares. You know that the areas you have found for these figures are the number of square units within each figure (cm2, in2, ft2, m2, and so on).

 

Watch “Area: Demonstration Applet.” This applet can be used to calculate areas for squares and rectangles. Areas are found both by counting unit squares and by applying the formula, which is a shortcut for finding out how many unit squares the rectangle contains.

 

Notice that the final number of squares counted is the same as the answer displayed for Area = length × width. Make rectangles with different dimensions to see that the number of squares counted is always the same as the area calculation provided on the right side of the applet.

 

Of course, not all areas are square or rectangular. The next applet illustrates how the area of an irregular two-dimensional (2-D) shape can be approximated by counting unit squares.

 

A 2-D shape can be drawn on a flat surface. A 2-D shape has length and width.

 

Watch the animation “Area Example: Area of a Figure.” Select [PLAY] to watch the animation.

 

On the right, the figure was broken up into parts and area formulas, which, as you will see in the next two lessons, are used to refine an estimate. In this lesson you will just count the squares to obtain the estimate. Notice that in the estimate there were 32 squares, which lay entirely within the figure. There were 50 squares that covered the entire figure.

 

A better estimate than either 32 or 50 unit squares is the average of these two estimates.

 

What is the average of 32 and 50? Remember, the average of two numbers is found by adding the numbers together and dividing the result by 2.

 

 

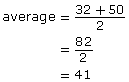
Notice how close this estimate, 41 units2, is to the calculated value of 40.

 

Try this technique to estimate the area of the 2-D shape in the next Self-Check question.

 

Self-Check

 

SC 4. Open and print “Irregular Two-Dimensional Shape.” You will need one copy to count the number of unit squares that are totally within the figure, and you will need a second copy to count the number of squares that totally cover the figure. Then find the average of the two counts. Hint: Make your count easier by using a highlighter to count the squares.

 

SC 5. If each square in the diagram is 1 cm on a side, what unit would your estimate have?

 

Compare your answers.

 

Mastering Concepts

 

Try these questions. When you are finished, check your answers.

 

© L Barnwell/shutterstock

 

Have you watched workers shingle a roof, or have you even helped shingle a roof? Asphalt shingles are sold by the square or by the bundle. A square is the number of shingles needed to cover 100 ft2—an area 10 ft by 10 ft. A bundle is one-third of a square. The weight of a bundle can be handled by one person.

 

MC 1. How many square feet are in a bundle?

 

MC 2. Contractors estimate that a bundle will normally cover 32 ft2, as there is always waste at the ends of the roof and by features such as chimneys and vents. If a bundle is of a square, how many square feet of shingles per square is allowed for waste?

 

MC 3. What percent of a square is allowed for waste?

 

MC 4. A roof is 1000 ft2 in area. How many bundles of shingles would a contractor estimate are needed to shingle that roof?

 

Compare your answers.

 

Mathematics 10-3 Learn EveryWare © 2010 Alberta Education