Module 4
1. Module 4
1.21. Page 4
Module 4: Area
Bringing Ideas Together
In Get Started and Explore you reviewed the nets of cubes, rectangular prisms, and pyramids. You can use nets to develop formulas for surface area.
 Self-Check
Self-Check
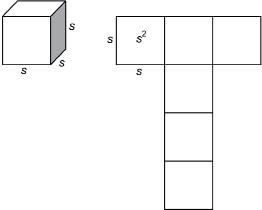
Take a look at the net for a cube with s units on a side.
Answer the following questions. When you are finished, check your answers.
SC 4. What do you notice about the areas of the squares in the net?
SC 5. How many squares make up the net for a cube?
SC 6. What would you suggest for the formula for the surface area of a cube?
Next, consider the net for a rectangular prism with length ![]() , width w, and height h.
, width w, and height h.
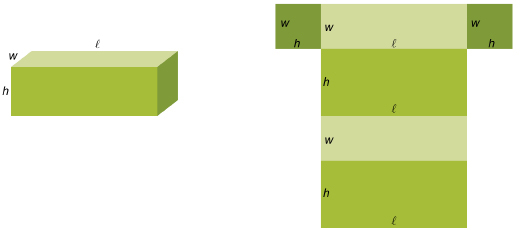
There are two faces with area ![]()
There are two faces with area ![]()
There are two faces with area hw.
So, the surface area of a rectangular prism is ![]()
If you worked on a rectangular prism in the Share activity, how does the formula you came up with compare with this formula?
Surface Area by Example
In the next few examples, you will sometimes apply these formulas and you will sometimes need to sketch the faces of the object to determine the surface area.

© Feng Yu/24837881/Fotolia
Example 1
What is the surface area of a sugar cube measuring 0.5 in on each side?
Solution
Each side, s, of the cube is 0.5 in.
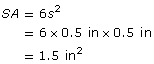
The surface area of this sugar cube is 1.5 in2.
This answer is reasonable because, if you rearranged the six faces of the cube, the faces would form one square with sides of 1 in and a rectangle half the area of the square.
Example 2
What is the surface area of a cardboard container 2 ft long, 18 in wide, and 1 ft high?
Solution
All dimensions must be in the same units.
![]()
So, ![]()
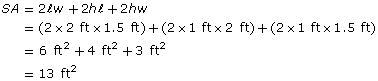
The surface area of the box is 13 ft2.
You could also solve this question using square inches. Since 1 ft is 12 in, 2 ft is 2 × 12 = 24 in. Then, ![]() = 24 in, w = 18 in, and h = 12 in.
= 24 in, w = 18 in, and h = 12 in.
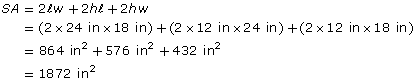
The surface area of the box is 1872 in2.
Example 3
What is the surface area of a pyramid with a square base measuring 10 cm on a side and 4 identical triangular faces with heights of 8 cm measured along the face?
Solution
In this solution you will see how to find the surface area of a pyramid. As you watch, pause the recording and try to predict the next step in solving the question.
View “Example 3 Solution.”
Example 4
Find the surface area of the triangular prism. Each triangular end is 4 cm along the base, 3 cm high, and 5 cm along the longest side. The prism is 10 cm long.
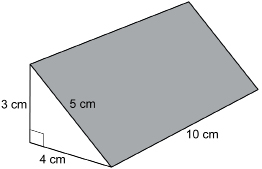
Solution
Sketch the faces of the prism and find their areas.
The base of the prism is a rectangle 10 cm by 4 cm.
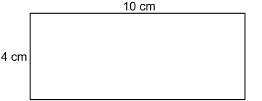
![]()
The back of the prism is a rectangle 10 cm by 3 cm.
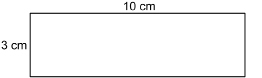
![]()
The slant face of the prism is a rectangle 10 cm by 5 cm.
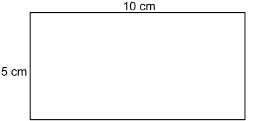
![]()
Each triangular end is a triangle with a base of 4 cm and a height of 3 cm.
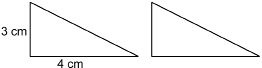
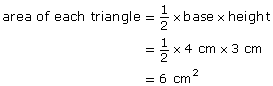
surface area of prism = area of base + area of back + area of slant face + (2 × area of triangle)
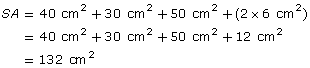
The area of the prism is 132 cm2.
Now check your mastery of surface area.
 Self-Check
Self-Check
Answer the following questions. When you are finished, check your answers.
SC 7. A cubical shipping carton is 30 in on a side. What is the carton’s surface area in cubic feet?
SC 8. Over 90% of non-bulk goods shipped by ship, rail, and truck are in rectangular containers. A common container is 48 ft long, 8 ft wide, and 8 ft high. What is the surface area of this container?
SC 9. Jim is going to paint the walls and ceiling of his room. His room is 9 ft wide, 12 ft long, and 8 ft high. He wishes to estimate the area he will cover in order to buy enough paint. What is Jim’s estimate? (Notice that Jim won’t be painting the floor. In doing your estimate, you can ignore the door and window in Jim’s room.)
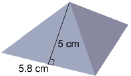
SC 10. A tetrahedron has 4 identical triangular faces. What is the surface area of the tetrahedron shown below?
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
Star plans to sew a slip cover for her couch. She needs to estimate the fabric required. How can she minimize her calculations?