Module 3 Project

Step 5

At the Winter Olympics in 1988, the winning men’s doubles luge team was Joerg Hoffmann and Jochen Pietzsch. They finished their two heats in a total time of 1:31.940.

The first-place time at Vancouver was given as 1:22.705. Andris Sics and Juris Sics placed second in Vancouver and had a time of 1:22.969.

1. Assume that the times from the Calgary Olympics and the Vancouver Olympics are proportional. What would be the time of the Calgary Olympics second-place finishers? You should use proportional reasoning to solve this problem. Round your answer to thousandths of a second. (5 marks)
   
   
2. Search the Internet for the second-place time in Calgary. Was the assumption valid that the times were proportional? (3 marks)

Step 6

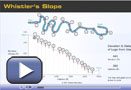
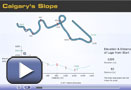
While working on the Module 3 Project in Lesson 2 of Section 1, you found the slope of different parts of the Whistler track and the Calgary track. You can use the Whistler's Slope and Calgary's Slope animations to discover other things about the track.

1. How many metres does the Whistler track fall over the first 900 ft? (3 marks)
   
   
2. How many metres is 900 ft? (2 marks)
   
   
3. How many metres does the luge track at Canada Olympic Park in Calgary fall in the first 900 ft? (3 marks)
   
   
4. How does the slope of the first 900 feet of the two tracks compare? (3 marks)

Summary

In a short paragraph, summarize why the Whistler track is faster than the Canada Olympic Park track. Base your summary on the data and calculations performed throughout the project’s six steps. (3 marks)