1. Lesson 1

1.5. Explore

Mathematics 30-3 Module 5

Module 5: Geometry

 

Explore

 

As you are aware, a triangle is a polygon made up of three sides. It is a very popular shape that is used in many structures for both aesthetics and its incredible strength.

 

The triangle is the strongest of all polygons since the length of each side is dependent on the other two sides, and the measurement of each angle within the triangle is dependent on the other two angle measurements. As you learned in the Try This 1 activity, you cannot change one measurement—be it the length of the side or angle measurement—without affecting the other measurements. The angles and sides act as reinforcements for one another, making the triangle very rigid and strong, hence the reason it is so popular in construction!

 

Triangles can be classified in two different ways—by angle measure and by side length.

 

Triangles Classified By Angle Measure
acute all three angle measures are less than 90° 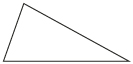This is an acute triangle.
obtuse one angle measure is greater than 90° This is an obtuse triangle.
right one angle measure is 90° 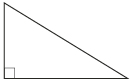This is a right triangle.

Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)

 

Triangles Classified By Side Length
equilateral three sides are of equal length and three angles are of equal measure 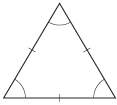This is an equilateral triangle.
isosceles two sides are of equal length and two angles are of equal measure 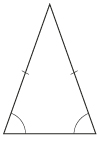This is an isosceles triangle.
scalene no sides are of equal length and no angles are of equal measure These are scalene triangles.

Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)

 

Did You Know?

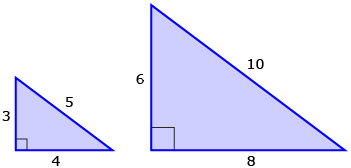
This is a diagram of two 3:4:5 triangles.

The 3:4:5 triangle is a right-angled triangle where the sides have a ratio of 3:4:5. The image shows some examples of 3:4:5 triangles, also known as Pythagorean triples.

 

The 3:4:5 triangle has been used for centuries, and it is claimed to be the special triangle used to construct the Great Pyramids of Giza.

 

This is a photograph of the Great Pyramids of Giza.

iStockphoto/Thinkstock

It appears the Egyptians were familiar with some mathematics that are still used today by carpenters and other tradespeople to square corners when a measuring device is not available. For example, a carpet installer may use the 3:4:5 triangle rule to ensure that the corners of a carpet that have been cut are indeed 90 degrees.