1. Lesson 1

1.7. Explore 3

Mathematics 30-3 Module 5

Module 5: Geometry

 

In Try This 2, you may have noticed the following point.

 

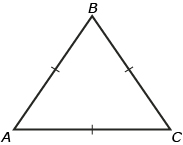
In an equilateral triangle all three angles are equal, so the measure of each angle would be 180° ÷ 3 = 60°.

 

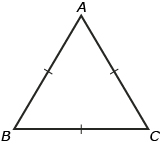
In the diagram,

 

 

∠A = 60°, ∠B = 60°, ∠C = 60°

 

This is a diagram of an equilateral triangle ABC.

 

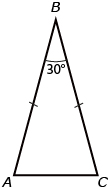
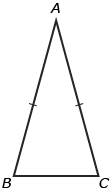
In an isosceles triangle, the interior angles opposite the equal sides are equal. In the diagram,

 

 

∠B = ∠C

 

This is a diagram of an isosceles triangle ABC.

 

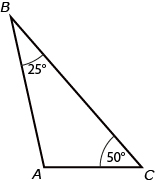
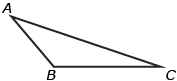
In a scalene triangle, as with all triangles, the three interior angles must add up to 180 degrees. If you know two of the angles, the third angle can be determined by subtracting the two known angles from 180. In the diagram,

 

 

∠A + ∠B + ∠C = 180°

 

This is a diagram of a scalene triangle ABC.

 

Read “Example 1” on page 182 of the textbook. As you read, notice how the unknown angles in each triangle are calculated.

 

Self-Check 1
  1. Answer “Build Your Skills” question 1 on page 187 of the textbook. Answer
  2. Answer “Build Your Skills” question 5 on page 189 of the textbook. Answer
  3. In each of the following triangles, solve for the missing angles and classify each triangle as
    1. scalene, isosceles, or equilateral
    2. acute, obtuse, or right
  1. This is a diagram of triangle ABC with 30 degrees at angle B.
    Answer

  2. This is a diagram of triangle ABC with 25 degrees at angle B and 50 degrees at angle C.
    Answer

  3. This is a diagram of triangle ABC with a right angle at B.
    Answer
  4. This is a diagram of triangle ABC.
    Answer