1. Lesson 3

1.5. Explore

Mathematics 30-3 Module 5

Module 5: Geometry

 

Explore

 

In Try This 1, you may have noticed the following properties of regular polygons.

  • All sides are equal.
  • All interior angles are equal.
  • If there is an even number of sides, then the opposite sides are parallel.
  • If there is an odd number of sides, then there are no parallel sides.
  • The number of lines of symmetry is equal to the number of sides.
Self-Check 1
  1. Open “Exploring Shape Classification” and complete Level 2.

     
    This is a play button that opens up Exploring Shape Classification.

 

textbook

  1. Answer “Build Your Skills” question 1 on page 207 of the textbook. Answer

 

So far you have looked at some of the properties of regular polygons. In the next Try This, you will take a closer look at the measure of the interior angles of regular polygons and how these angles can be determined.

 

Try This 2

 

Open Regular Polygons and use the Size slider to change the size of each regular polygon.

 

 

This is a play button that opens up Regular Polygons.

  1. If the lengths of the sides of a regular polygon change, do the interior angles change? Explain.

Use the following information and the image to answer the remaining questions.

Each interior angle of a regular pentagon is 108°. You will discover how this measurement can be calculated using triangle properties.

 

 
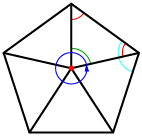
This is a regular pentagon with the centre indicated with a red dot.
  1. From the centre of the pentagon, draw line segments to each vertex, similar to the diagram shown. How many triangles are formed? Are the triangles identical? Why or why not?
  2. At the centre of the pentagon, the triangles meet. What is the angle indicated in dark blue at the centre of the pentagon?
  3. Using your answers from questions 2 and 3, what is the measure of the angle of each triangle where it touches the centre of the pentagon (indicated in green)?
  4. What type of triangles are formed inside the regular pentagon?
  5. Using your answers from questions 4 and 5, what are the measures of the angles inside the triangle, indicated in red at the outer edges of the triangle?
  6. What is the measure of each interior angle of the pentagon (indicated in light blue)?
  7. What is the sum of the interior angles of the pentagon?

course folder Save your responses in your course folder.

This angle is one full rotation of a circle.