1. Lesson 3

1.6. Explore 2

Mathematics 30-3 Module 5

Module 5: Geometry

 

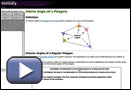
In Try This 2, you may have found that the triangles created inside a regular pentagon are identical and are isosceles triangles. Using your knowledge of isosceles triangles, you would have determined the measure of each interior angle of the regular pentagon. To see how the interior angle of a regular polygon can be determined, view Interior Angles of a Regular Polygon. Select the Play button for each step to continue.

 

 

This is a play button that opens Interior Angles of a Regular Polygon.

As you saw in Interior Angles of a Regular Polygon, the measure of each interior angle and the sum of the interior angles of a regular polygon can be determined using the formulas given here.

 

For an n-sided regular polygon, the following are true:

 

 


 
the sum of interior angles = 180°(n − 2)

 

In the next Try This, you will use these formulas to determine the measure of each interior angle and the sum of the interior angles for regular polygons.

 

Try This 3
  1. Complete a table like the one shown.

    Regular Polygon Name Number of Sides, n Measure of Each Interior Angle Sum of Interior Angles

    This is a blue triangle.

     

    		 equilateral triangle 3    

    This is a red square.

     

    		 square 4    

    This is a yellow pentagon.

     

    		 pentagon 5    

    This is a green hexagon.

     

    		 hexagon 6    

    This is a brown octagon.

     

    		 octagon 8    

    This is a purple decagon.

     

    		 decagon 10    
  2. What happens to the measure of each interior angle as the number of sides increases?
  3. Create a graph with the data from your table. Graph the number of sides, n, on the x-axis and the sum of interior angles, S, on the y-axis.
  4. What happens to the sum of the angles as the number of sides increases?

course folder Save your responses in your course folder.