Lesson 4

Explore

 

A transformation is the movement of a shape or object by sliding, flipping, rotating, or changing its size. In Try This 1, you were introduced to four types of transformations:

• translations
• reflections
• dilations
• rotations

In this lesson, you will explore these types of transformations one at a time.

---

A translation is the horizontal and/or vertical movement of an object. Translations are useful when you would like to reproduce the same shape but in a different location. The next activity will explore a rule that can be used for translations.

 

Try This 2

 

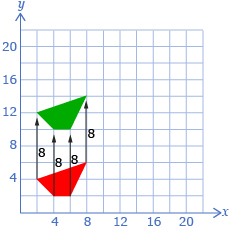
Suppose you are building a beanbag game where the object of the game is to throw a beanbag through a hole. You have drawn a quadrilateral as the shape of the hole you would like to use, but now you need to draw this quadrilateral in three other locations. You would like the centre of each quadrilateral to be a specified distance apart, as shown in the diagram.

 

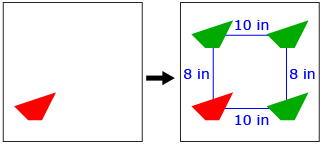
1. Describe a strategy that can be used to draw the three remaining quadrilaterals.
2. How accurate do you feel your strategy will be? Can you think of a more accurate strategy?

There are many reasonable ways to draw the remaining quadrilaterals. One possibility is to use a coordinate grid. The grid can be used to count the distances.

3. Make a grid with a quadrilateral like the one shown here. Use your grid to draw the three remaining shapes.
   
   
   
   
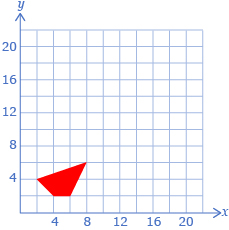
4. For each quadrilateral, label the vertices with their coordinates.
5. Describe how the coordinates of the original quadrilateral are related to those of the new quadrilaterals. The following table may help organize your thinking.
   
   

   Quadrilateral	How the Coordinates Are Related to Those of the Original
   8 units up from the original
   10 units right from the original
   8 units up and 10 units right from the original

6. What happens to the coordinates of the original quadrilateral when the quadrilateral is moved as follows?
   • right 18
   • down 6
   • left 8
   • down 10 and left 12

Save your responses in your course folder.

 

Share 1

 

With a partner or in a group, discuss the following questions.

1. Compare the strategies you used to move the quadrilaterals in the coordinate grid. Explain which strategy you feel is more accurate.
2. Describe an advantage of using just coordinates instead of drawings to describe the translation of an object.

If required, place a summary of your discussion in your course folder.