Lesson 4

Rotations are the final type of transformation for you to explore. A rotation is the movement of an object around a fixed point. A rotation is useful if you want to change the orientation of an object by a specific amount. Rotations are often used in pattern generation.

Try This 5

1.  Consider this diagram:
   
   
    
   
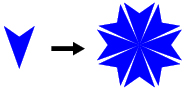
   1. Describe a strategy you could use to accurately draw the second diagram using the first diagram.
   2. How accurate do you expect your diagram to be?

2. There are many ways to complete the design in question 1. One way is to use rotations. Open Rotations. You can use the polygon provided, or make your own polygon by moving the vertices. Move the slider to rotate the polygon about the origin.
   
   
    
   
   1. Describe what happens when you rotate the polygon clockwise and counterclockwise.
   2. How is the point (0, 0) special for this rotation? Why is it called the centre of rotation?
   3. How is a rotation of 90° clockwise related to a rotation of 270° counterclockwise?
3. The positions of points after rotations of 90°, 180°, and 270° can be predicted using methods similar to those for other transformations.
   1. Complete a table like the one shown using three points from your polygon.
      
      

      Original Point	Point After 90° Rotation Clockwise	Point After 180° Rotation Clockwise	Point After 270° Rotation Clockwise

   2. Describe how the original point is related to the corresponding point after each of the three rotations.
   3. Use your answers from part b. to predict a rule that describes how the points change for each angle. The following table may help organize your thinking.
      
      

      90° Rotation Clockwise	180° Rotation Clockwise	270° Rotation Clockwise

   4. Do you expect the rules you determined in part c. to work for counterclockwise rotations? If not, provide a set of rules that will work.

Save your responses in your course folder.