1. Lesson 6

Mathematics 30-3 Module 5

Module 5: Geometry

 

Lesson 6: Sine Law

 
Focus

 

This is a photograph of a trig point.

Hemera/Thinkstock

When you used the sine ratio in previous courses, you were working with right triangles. Not all problems involve right triangles. For instance, the original maps of Britain were based on survey work done between 1783 and 1853. In the early twentieth century, the British government realized that their maps were not completely accurate and decided to create new maps for all of Britain.

 

The triangulation method of surveying was used to complete the Retriangulation of Britain (1935–1962). Concrete pillars called trig points were created all around the country. These pillars became the vertices of triangles that were used to create accurate maps of Britain. Trigonometry played an important role in helping to calculate the angles and distances between trig points.

 

Trig-point locations were chosen for maximum visibility—the British didn’t have the luxury of creating right triangles. As a result, mathematics that is valid for all triangles, including oblique (non-right-angled) triangles, was used.

 

Today, if you were to use triangulation to measure distances around Lesser Slave Lake, you might end up with trig points and corresponding triangles at the locations shown.

 

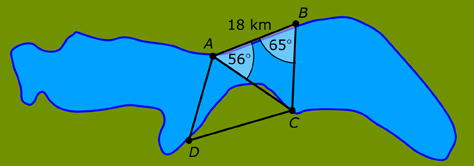
This diagram shows Lesser Slave Lake with four trig points and the two triangles that can be formed from these.

 

There are no right-angled triangles in this diagram. You need to be certain that the method for solving this problem is valid for oblique (non-right-angled) triangles.

 

Lesson Outcomes

 

At the end of this lesson you will be able to

  • use the sine law to determine an unknown length
  • use the sine law to determine an unknown angle
Lesson Question


You will investigate the following question:

  • How can the sine law be used to determine unknown sides and angles of oblique triangles?
Assessment

 

Your assessment may be based on a combination of the following tasks:

  • completion of the Lesson 6 Assignment (Download the Lesson 6 Assignment and save it in your course folder now.)
  • course folder submissions from Try This and Share activities
  • additions to Glossary Terms and Formula Sheet
Materials and Equipment
  • calculator