Lesson 6
1. Lesson 6
1.5. Explore
Module 5: Geometry
Explore
In Try This 1, you explored a relationship that can be used with any triangle. This relationship is called the sine law and is often written as
![]()
![]() can also be written as
can also be written as ![]()
Again, this represents three separate equations:
In some situations, one version of the sine law is easier to use than the other.
Another way of writing this equation is to break it into three separate equations:
![]() means that the length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle.
means that the length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle.
Watch Sine Law Illustrator to see this pictorially.
The sine law formulas reflect how mathematicians typically label triangles: sides are named with lowercase letters and angles are named with uppercase letters. Sides and their opposite angles are named with the same letter—for example, b and B.
You may find it helpful to view How to Label a Triangle.
The sine law can be used to determine an unknown length in a triangle. Typically, the equations with the sines in the denominator are easiest to use when determining an unknown length. Try This 2 explores this idea.
Try This 2
- Draw the following triangle.
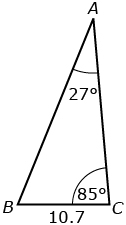
- Label the sides of the triangle with a, b, and c using the method described in How to Label a Triangle.
- Determine which of the following versions of the sine law would be best to find the length of the side between A and B. Explain your choice(s).

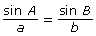
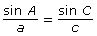
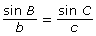
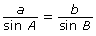
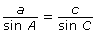
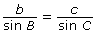
- Use your choice from part b. to determine the length of the side between A and B.

- Explain how you could determine the third angle of the triangle using the first two angles.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Writing a list of known values for the sides and angles of the triangle may be helpful. Place a “?” with the side you are trying to determine. One side and one angle will be left blank.
| Sides a = 10.7 b = c = ? |
Angles A = 27° B = C = 85° |