1. Lesson 6

1.7. Explore 3

Mathematics 30-3 Module 5

Module 5: Geometry

 

This is a photo of a compass on a map.

iStockphoto/Thinkstock

It is also possible to use the sine law to determine an unknown angle. The sine law equations with the sines in the numerator are typically easiest to use for determining unknown angles.

 

The following example shows how this can be done. Pay attention to when sin−1 is used while solving the problem.

 

Jeremy is learning how to use a compass in an orienteering course. The instructions he was given tell him that he must walk 70 m from checkpoint A to checkpoint B. He knows that checkpoint A is directly north of his location at checkpoint c, and checkpoint B is in a direction of N41°E. He also knows that checkpoint B is 105 m from checkpoint C. He begins by drawing a diagram to represent his situation.

 

 

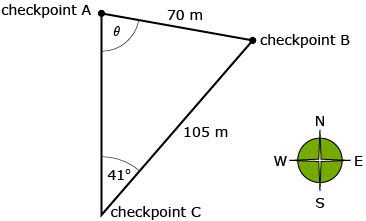
This diagram shows three checkpoints. Checkpoint A is directly above Checkpoint C. The angle at Checkpoint A is labelled theta and the angle at Checkpoint C is 41 degrees. Checkpoint A is 70 metres from Checkpoint B and Checkpoint C is 105 metres away from Checkpoint B. There is a directional star indicating that up is north.

 

 

Jeremy needs to determine the direction to walk when going from checkpoint A to checkpoint B.

 

Did You Know?

Orienteering is a sport where participants use a map and compass to find checkpoints or control points in an unfamiliar area. Orienteering is commonly done on foot, but other forms of transportation are possible.

 

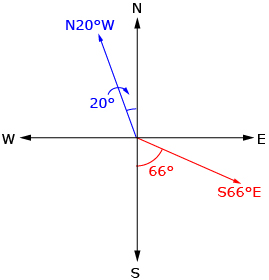
When using a map and compass, one method of giving a direction is to use angles from north or south. For example: “N20°W” means start facing north and turn 20° towards the west. “S66°E” means start facing south and turn 66° towards the east.

 

This diagram shows that “N20°W” is 20 degrees to the west of north and that “S66°E” is 66 degrees to the east of south.

 

From the diagram he drew, he knows that once he determines ∠θ he will be able to state the direction as Sθ°E. Jeremy looks at the given information and recognizes that he can use the sine law to determine this angle. His solution can be seen in the animation Jeremy’s Solution.

 

 

This play button opens Jeremy's Solution.

 

When solving a sine law equation for an angle θ, you need to isolate sin θ and then use sin−1 on both sides of the equation.

 

Note that sin−1 is often the second function of the sin button on your calculator. Sometimes sin−1 is written as “arcsin” on calculators.

 

The equation sin θ = 0.5 can be solved for θ using the following steps:

 

 

 

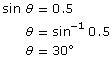
Check that you get sin−1 0.5 = 30 on your calculator.

 

In the next activity, you will correctly order the steps for determining an angle using the sine law.