Lesson 4

Explore

 

In Try This 1, you looked at permutations and combinations of ice cream cones. The number of combinations is the number of ways you can select items from a group when order does not matter. In the Two Scoops interactive, a chocolate-strawberry cone is the same as a strawberry-chocolate cone.

 

You may have noticed in Discover that the notation for combinations is similar to that of permutations.

 

	Notation	Order	Ice Cream Cone Possibilities
Combination	nCr	order does not matter	4C2 = 6
Permutation	nPr	order matters	4P2 = 12

 

In Try This 1, nCr represents taking r objects (2 flavours) from a group of n (4 possible flavours) when the order does not matter. In nPr, the restriction on r is r ≤ n. This is also true for nCr because you can’t choose more objects than are available.

 

In the following Try This 2, you will explore combinations and how they compare to permutations.

 

Try This 2

 

Step 1: Open the Permutations and Combinations gizmo from LearnAlberta.

 

Screenshot reprinted with permission of ExploreLearning

 

This gizmo represents the number of ways you can take items from a box. It also allows you to decide whether to pay attention to the order or not. This is an added feature as compared to the gizmo you used in Lesson 3.

 

Step 2: Set “Number of tiles in box” to 3.

 

Step 3: Set “Number of draws from box” to 2, and select “Yes” to indicate that the order is important. This setting corresponds to the first line of the table you will complete in step 5.

 

Step 4: Choose “Simulate.” Switch between the tabs at the top for different representations of the information.

Screenshot reprinted with permission of ExploreLearning

 

 

Step 5: Complete the following table.

Tiles	Draws	Is Order Important?	Number of Possibilities	Sketch of Tree Diagram	Notation	Permutation or Combination
3	2	Yes	6		3P2	Permutation
3	2	No
5	2	Yes
5	2	No		Do not draw.
4	3	No		Do not draw.
4	4	No		Do not draw.
5	5	No		Do not draw.

 

Save your answers to your course folder.

 

Share 2

 

With a partner or group, discuss the following questions based on what you discovered in Try This 2.

1. How did the tree diagram change when you switched from order being important to not important?
2. Why are there fewer combinations of a specified number of items as compared to the number of permutations?
3. The interactive shows that the permutation and combination formulas are related by 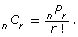Explain why dividing the number of permutations by r! gives the number of combinations.
4. Think of a real-life example where you would be interested in the number of combinations instead of permutations.

If required, save a record of your discussion in your course folder.