1. Lesson 4

Mathematics 30-2 Module 3

Module 3: Permutations, Combinations, and the Fundamental Counting Principle

 

Lesson 4: Solving Problems That Involve Combinations

 
Focus

 

This is a photo of a male figure holding a magnifying glass.

iStockphoto/Thinkstock

In his book The Codebreakers: The Story of Secret Writing, David Kahn tells the story of how a New York City detective broke up a betting ring. The detective observed a bookie taking bets all day and writing them down. However, when the detective made the arrest, much to his surprise, the list did not consist of names and amounts of bets but rather a series of musical notes. Convinced that the notes must be a code, the detective took the list for cryptanalysis. Sure enough, when the notes were played it did not result in beautiful music. Indeed, the notes were a code! The detective broke the code and solved his case.

 

There have been cases of music notes being used to deliver hidden messages. The code might be in the music lyrics or within the notes themselves.

 

The piano is one of the most common musical instruments in the world. A typical keyboard has 88 keys with a repetitive naming sequence as shown in the diagram. Keys with the same name, such as two A notes, sound similar, but one note is higher than the other.

 

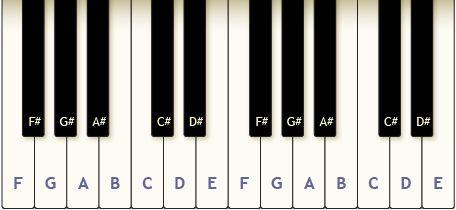
This diagram shows two octaves of a piano keyboard with the keys labelled.

This illustration shows part of a piano keyboard.

 

A chord can be produced on a piano when more than one key is pressed at the same time. How could you determine the number of different chords a piano can produce? What if you wanted chords using only the white keys? Suppose the pianist’s fingers could only span eight white keys. How could you determine how many one-handed chords could be produced?

 

In the previous lesson you examined permutations—that is, the number of ways objects can be arranged when order is important. But on the piano, the order a chord is written in or played does not change its sound. ACE is the same as CAE since all keys are pressed at the same time in a chord.

 

This diagram shows one octave of a piano keyboard. The A, C, and E keys are highlighted.

 

In this lesson you will explore a method of determining the number of ways to select objects if the order is not important.

 

Lesson Outcome

 

At the end of this lesson, you will be able to determine the number of combinations of elements given certain criteria.

 

Lesson Questions

 

In this lesson you will investigate the following questions:

  • What are the similarities and differences between permutation and combination problems?
  • How are problems involving combinations solved?
Assessment

 

Your assessment may be based on a combination of the following tasks:

  • completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
  • course folder submissions from Try This and Share activities
  • additions to Glossary Terms and Formula Sheet
  • work under Project Connection