Lesson 4
Completion requirements
Created by IMSreader
1. Lesson 4
1.9. Explore 5
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Hemera/Thinkstock
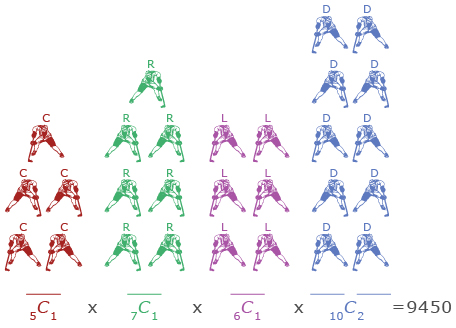
In Try This 3, the coach must choose a centre and a right-winger and a left-winger and 2 defensemen. By using the fundamental counting principle, you multiply the number of choices for each position to determine the total number of ways to make these choices.
- centre: 5C1 = 5
- right-winger: 7C1 = 7
- left-winger: 6C1 = 6
- two defensemen: 10C2 = 45
The total number of ways the coach can choose the first line is 5 × 7 × 6 × 45 = 9450 ways.
If you would like to see another example of a permutation question with extra conditions placed on it, read part b of “Example 3” on pages 114 and 115 of your textbook. As you read, note how the word and indicates that the two combinations must be multiplied to find the total number of combinations.
Self-Check 3
- Complete question 12 on page 119 of your textbook. Answer
- The student activities committee consists of 5 students from Grade 10, 5 students from Grade 11, and 8 students from Grade 12. There are also 2 teachers on the committee. How many dance subcommittees can be formed if there must be 2 students from each grade and 1 teacher? Answer