Lesson 4

Remember that in some of the permutation calculations in Lesson 3, you used cases. Cases can be used to split a solution into different possible scenarios. Because you can have the first scenario or the second scenario, you add the number of permutations in each case to determine the total. There are also some combination questions that require the use of cases. Consider the following example.

Pianists can create different chords by pressing several keys down at the same time on a piano.

How many chords are possible in each situation?

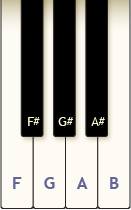
• Using the keys from the piano as shown, how many different chords—combinations of two or more keys—can be produced using exactly 4 fingers if each finger only presses 1 key, black or white, at a time?
• How many chords can be produced using 3 or 4 fingers?
• How many chords can be produced using 2 or 3 or 4 fingers?

Watch Piano Chords to see how the number of chords can be calculated for each situation.