1. Lesson 1

1.5. Explore

Mathematics 30-2 Module 4

Module 4: Polynomials

 

Explore

 

The shapes of the functions you experimented with in the Discover section are summarized in the following table.

 

Type of Function

Highest Exponent

Example Equation

Example Shape

Constant

0

f(x) = −2

This graph shows a horizontal line below the x-axis.

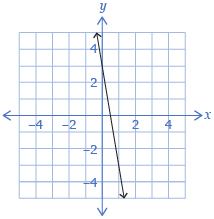
Linear

1

f(x) = −5x + 3

This graph shows a straight line going from quadrant 2 to quadrant 4.

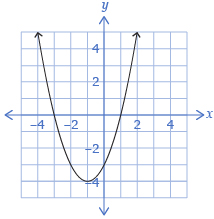
Quadratic

2

f(x) = x2 + 2x − 3

This graph shows a parabola opening up with vertex in quadrant 3.

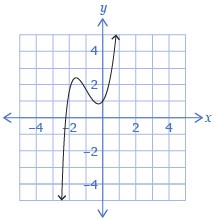
Cubic

3

f(x) = 2x3 + 5x2 + 2x + 1

This graph shows a curve starting in quadrant 3, increasing into quadrant 2, decreasing into quadrant 1, and then increasing into a higher area of quadrant 1. 

 

 

The functions you graphed in the Discover are all examples of polynomial functions.

 

A polynomial function contains only the operations of multiplication and addition with real numbers and variables. For example,

 

 

f(x) = 5x3 + 6x2 − 3x + 7

 

The function can also be written as

 

 

f(x) = 5(x)(x)(x) + 6(x)(x) + (−3)x + 7

 

From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.


 

In Discover you specified the highest exponent (on a variable). This is called the degree of the polynomial. In this module you will work with degree 0, 1, 2, and 3 polynomial functions.

 

Degree

Name

Example

0

constant

f(x) = 3.5

1

linear

f(x) = 4x − 1

2

quadratic

f(x) = 3x2 + 6x − 1

3

cubic

f(x) = 5x3 − 4x2 + 7x + 3

 

Try This 1 introduced you to the general shapes and characteristics of polynomial functions. When describing a graph, it is often useful to consider the following characteristics:

  • x-intercepts
  • y-intercepts
  • end behaviour
  • domain
  • range
  • turning points

Most of these characteristics should be familiar to you; however, end behavior and turning points may be new.

 

The end behaviour of a graph describes what happens as the x-values become very large positive or very large negative numbers. In this course, you will typically describe end behaviour by stating the quadrant the graph is in for large negative x-values and large postive x-values.

 

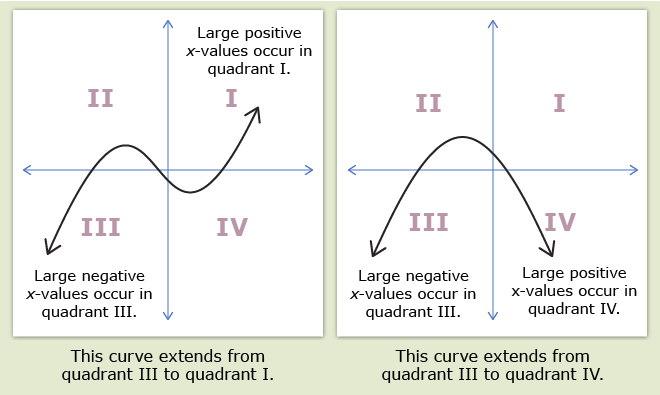
This diagram shows two functions. The first function extends from quadrant III to quadrant I. A label in quadrant III states “large negative x-values occur in quadrant III,” and a second label in quadrant IV states “large positive x-values occur in quadrant I.” The second function extends from quadrant III to quadrant IV. A label in quadrant III states “large negative x-values occur in quadrant III,” and a second label in quadrant IV states “large positive x-values occur in quadrant IV.”

 

A turning point occurs when a graph changes from increasing to decreasing or from decreasing to increasing.

 

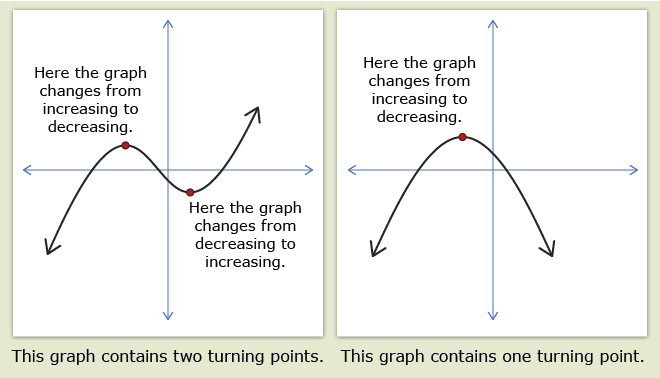
This diagram shows two functions. The first has two turning points, one showing the graph changing from increasing to decreasing and one changing the graph from decreasing to increasing. The second graph has one turning point where the graph changes from increasing to decreasing.

 

tip

In the definition for turning point, describing a function that is decreasing means the curve is falling from left to right. Describing a function that is increasing means the curve is rising from left to right.