1. Module 4 Summary

Mathematics 30-2 Module 4

Module 4 Summary

 

This shows a picture of kite surfing at a beach.

iStockphoto/Thinkstock

Polynomial functions can be used to model many real-world problems. In this module you

  • sketched representative graphs of linear, quadratic, and cubic polynomial functions
  • related characteristics of graphs of polynomial functions to the functions’ algebraic forms
  • used technology to determine equations of lines and curves of best fit
  • used regression equations to answer questions in real-world contexts

In the Module 4 Project you explored and analyzed shapes of polynomials found in our environment.

 

Following are some of the key ideas you learned in each lesson.

 

 

 

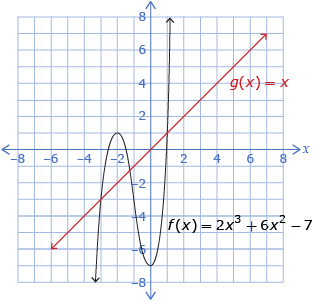
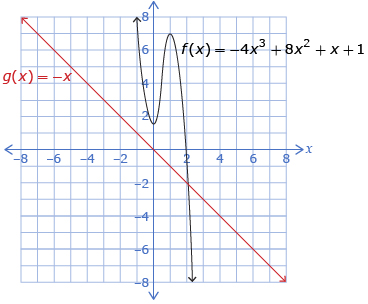
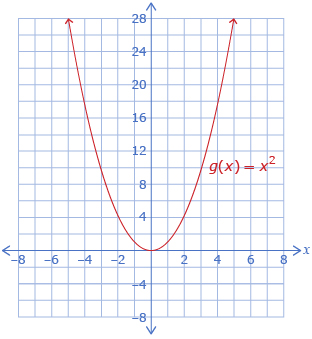
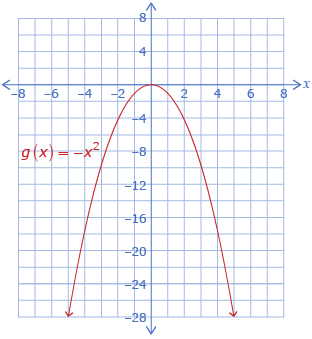
Lesson 1

The general shape of the graph of a polynomial function is determined by the type of function (linear, quadratic, cubic) and the sign of the leading coefficient.

 

Linear and Cubic, Positive Leading Coefficient

This shows the graphs of g of x equals x and f of x equals two x cubed plus 6 x squared minus 7.

 

Linear and Cubic, Negative Leading Coefficient

 

This shows the graphs of g of x equals negative x and f of x equals negative 4 x cubed plus 8 x squared plus x plus 1.

 

Quadratic, Positive Leading Coefficient

 

This shows the graph of g of x equals x squared.

 

Quadratic, Negative Leading Coefficient

 

This shows the graph of g of x equals negative x squared.
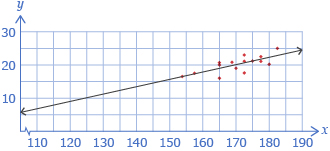
Lesson 2

Lines of best fit can be created for data that exhibits a linear trend.

 

This shows a scatter plot that exhibits a linear trend. A line of best fit is shown going through the middle of the data.
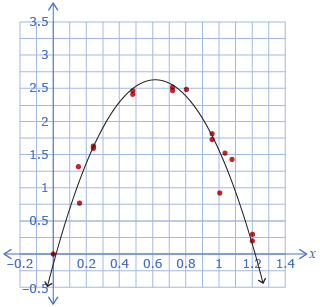
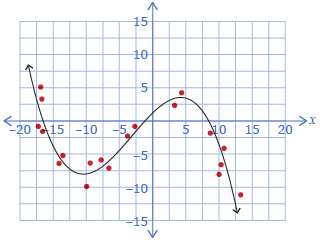
Lesson 3

Curves of best fit can be created for data that exhibits quadratic or cubic trends.

 

Quadratic Trend

This shows a scatter plot that exhibits a quadratic trend. A curve of best fit is shown going through the middle of the data.

 

Cubic Trend

 

This shows a scatter plot that exhibits a cubic trend. A curve of best fit is shown going through the middle of the data.